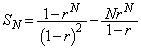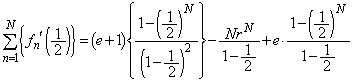福井大医数学'11年[4]
関数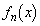
(
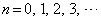)は次の条件を満たしている。
このとき、以下の問いに答えよ。
(1) 
，
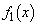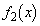を求めよ。 (2) 
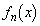の具体的な形を推測し、その結果を数学的帰納法で証明せよ。 (3) 
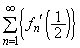を求めよ。ただし、
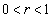に対して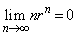
となることを用いてよい。
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
解答 単なる数Ⅲの総合計算問題に見えるのですが、やってみると、工夫が必要になる問題です。
(1) (ii)において、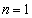
とすると、 ∴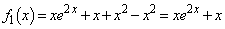 
......[答]
(ii)において、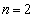
とすると、 
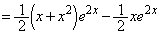(∵ ①)∴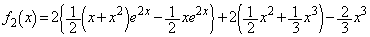 
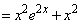......[答]
(2) (1)の結果より、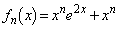
(
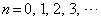)と予測できます。この予測を数学的帰納法によって証明します。 (Ⅰ)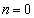 
のとき、(i)より、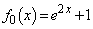
よって、予測は成立します。
(Ⅱ)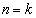 
のとき、予測が成立するとして、 が成立します。
ここで、単純素朴に、(ii)で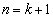
として、 
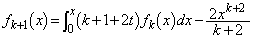･･･②を計算しようとしても、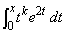
という形の積分が出てきて困ります。そこで、先回りして、 ∴ 
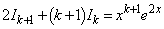･･･③
さて、②に、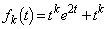
を代入すると、 よって、予測は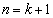
においても成立します。 (Ⅰ)，(Ⅱ)より、予測：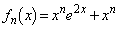
(
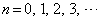)が成立することが証明されました。
(3) (2)より、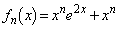
(
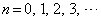) これを利用すると、④より、
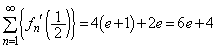......[答]
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
数学TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2024(有)りるらる 苦学楽学塾 随時入会受付中！理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。 
(
)
･･･①
(∵ ③)
の漸化式を考えることにします
として、
，