��嗝�n���w'11�N�O��[5]
����r�ɑ��āA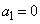 �C
�C �Ƃ����A����
�Ƃ����A���� �����̑Q�����Œ�߂�B
�����̑Q�����Œ�߂�B
������ ��
��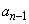 ����Q������p����
����Q������p����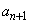 �����߂�ۂɂ͍d�݂𓊂��A�\���o���Ƃ�
�����߂�ۂɂ͍d�݂𓊂��A�\���o���Ƃ� �C�����o���Ƃ�
�C�����o���Ƃ� �Ƃ���B�����ŕ\���o��m���Ɨ����o��m���͓������Ƃ���B
�Ƃ���B�����ŕ\���o��m���Ɨ����o��m���͓������Ƃ���B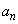 �̊��Ғl��
�̊��Ғl�� �Ƃ���Ƃ��A�ȉ��̖₢�ɓ�����B
�Ƃ���Ƃ��A�ȉ��̖₢�ɓ�����B
(1)  �����
����� ���Ar��p���ĕ\���B
���Ar��p���ĕ\���B (2)  �̂Ƃ���
�̂Ƃ���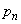 ���An��r��p���ĕ\���B
���An��r��p���ĕ\���B (3) ����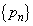 ����������悤�Ȑ���r�͈̔͂����߂�B
����������悤�Ȑ���r�͈̔͂����߂�B (4) r��(3)�ŋ��߂��͈͂��Ƃ��A�Ɍ��l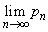 �̍ŏ��l�����߂�B
�̍ŏ��l�����߂�B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@�m���őQ�����̎��̍������߂�Ƃ�������ɋ�������܂����A�d�ʋ��̌v�Z���ł��B
(1) �d�݂𓊂��ĕ\���o���Ƃ��A
 (
( �Ƃ��܂�)
�Ƃ��܂�)�d�݂𓊂��ė����o���Ƃ��A
 (
(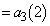 �Ƃ��܂�)
�Ƃ��܂�)�\���o��m���A�����o��m���͂Ƃ���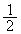 �Ȃ̂ŁA
�Ȃ̂ŁA �����Ғl
�����Ғl �́A
�́A 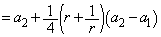 �@����@
�@����@ ......[��]
......[��]�d�݂�2���āA�\�A�\�Əo���Ƃ��A
 (
(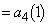 �Ƃ��܂�)
�Ƃ��܂�)�d�݂�2���āA�\�A���Əo���Ƃ��A
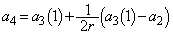 (
( �Ƃ��܂�)
�Ƃ��܂�)�d�݂�2���āA���A�\�Əo���Ƃ��A
 (
( �Ƃ��܂�)
�Ƃ��܂�)�d�݂�2���āA���A���Əo���Ƃ��A
 (
( �Ƃ��܂�)
�Ƃ��܂�)��L�ŁA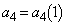 �C
�C �C
�C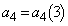 �C
�C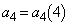 �ƂȂ�m���͂������
�ƂȂ�m���͂������ �ŁA
�ŁA �̊��Ғl
�̊��Ғl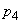 �́A
�́A 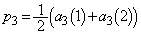 ���A
���A���ӁD �̏ꍇ�ɁA
�̏ꍇ�ɁA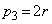 �C
�C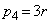 �ƕ����ĉ��Ă���{������܂����A��L�̉ŁA���̏ꍇ���܂�ł���̂Œ��ӂ��Ă��������B
�ƕ����ĉ��Ă���{������܂����A��L�̉ŁA���̏ꍇ���܂�ł���̂Œ��ӂ��Ă��������B
(2) �@�C�A���琔��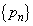 ���������Q�����̌`���\���ł��܂��B�����ŁA��ʓI�ꍇ�ɂ��āA�Q�������l���܂��B
���������Q�����̌`���\���ł��܂��B�����ŁA��ʓI�ꍇ�ɂ��āA�Q�������l���܂��B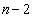 ��d�݂𓊂����Ƃ��A
��d�݂𓊂����Ƃ��A ���Ƃ蓾��
���Ƃ蓾�� �ʂ�̒l��
�ʂ�̒l��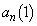 �C
�C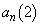 �C����C
�C����C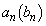 �Ƃ��܂��B
�Ƃ��܂��B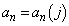 (
(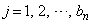 )�ɑ��āA�d�݂�1���āA�\���o��Ƃ�
)�ɑ��āA�d�݂�1���āA�\���o��Ƃ�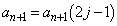 ����܂�A�����o��Ƃ�
����܂�A�����o��Ƃ�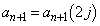 ����܂�Ƃ���A
����܂�Ƃ���A �́A
�́A �C
�C �C����C
�C����C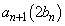 �́A
�́A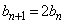 �ʂ�̒l���Ƃ蓾�܂��B
�ʂ�̒l���Ƃ蓾�܂��B 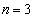 �̂Ƃ��A
�̂Ƃ��A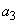 ��2�ʂ�̒l���Ƃ�A
��2�ʂ�̒l���Ƃ�A �̂Ƃ��A
�̂Ƃ��A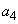 ��4�ʂ�̒l�����̂ŁA
��4�ʂ�̒l�����̂ŁA �́A
�́A �ʂ�̒l�����(
�ʂ�̒l�����( ��
�� �ʂ�A
�ʂ�A ��
�� �ʂ�)�A�e�l���Ƃ�m����
�ʂ�)�A�e�l���Ƃ�m���� �ł��B
�ł��B
�����ŁA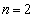 �̂Ƃ��A
�̂Ƃ��A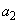 ��1�ʂ�̒lr���Ƃ�A
��1�ʂ�̒lr���Ƃ�A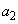 �̊��Ғl
�̊��Ғl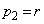 �Ƃ��܂��B
�Ƃ��܂��B
���āA �̂Ƃ��A
�̂Ƃ��A ��d�݂𓊂��āA
��d�݂𓊂��āA (
( )����A2��d�݂𓊂����Ƃ��̏��l���܂��B
)����A2��d�݂𓊂����Ƃ��̏��l���܂��B
�\�A�\�Əo���Ƃ���ƁA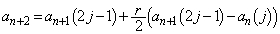 (
( �Ƃ��܂�)
�Ƃ��܂�)�\�A���Əo���Ƃ���ƁA
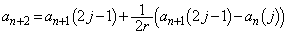 (
( �Ƃ��܂�)
�Ƃ��܂�)���A�\�Əo���Ƃ���ƁA
 (
(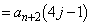 �Ƃ��܂�)
�Ƃ��܂�)���A���Əo���Ƃ���ƁA
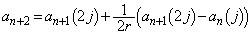 (
( �Ƃ��܂�)
�Ƃ��܂�)���ǁAn��d�݂𓊂����Ƃ��A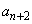 �́A
�́A �C
�C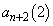 �C����C
�C����C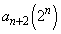 �Ƃ����l���Ƃ蓾�܂����A���̊m���͂������
�Ƃ����l���Ƃ蓾�܂����A���̊m���͂������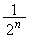 �ł��B
�ł��B �̊��Ғl
�̊��Ғl �́A
�́A  �@(
�@( )�@����B
)�@����B�����ŁA �̂Ƃ��A�܂�A
�̂Ƃ��A�܂�A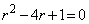 �C
�C �̂Ƃ��A�B�́A
�̂Ƃ��A�B�́A 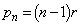 (
(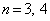 �̂Ƃ���OK)�@......[��]
�̂Ƃ���OK)�@......[��] �C�܂�A
�C�܂�A �̂Ƃ��A�B���A
�̂Ƃ��A�B���A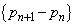 �́A�����F
�́A�����F �C����
�C����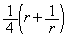 �����䐔���ł��B
�����䐔���ł��B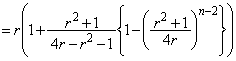 (
(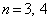 �̂Ƃ���OK)�@......[��]
�̂Ƃ���OK)�@......[��]
(3) 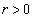 �Ȃ̂ŁA
�Ȃ̂ŁA �̂Ƃ��A
�̂Ƃ��A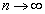 �Ƃ���ƁA
�Ƃ���ƁA �͔��U���܂��B
�͔��U���܂��B 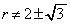 �̂Ƃ��A
�̂Ƃ��A �ł���A
�ł���A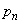 �͎������܂��B
�͎������܂��B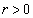 �ƁA
�ƁA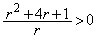 ����
���� 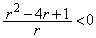
���A���� ����������r�͈̔͂́A
����������r�͈̔͂́A
(4) 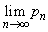 ����������Ƃ��A�܂�A
����������Ƃ��A�܂�A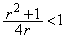 �C
�C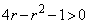 �̂Ƃ��A
�̂Ƃ��A ����́A �̂Ƃ��A�ŏ��l
�̂Ƃ��A�ŏ��l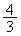 ......[��] ���Ƃ�܂��B
......[��] ���Ƃ�܂��B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B 
 �C
�C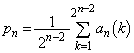 ���A�A��
���A�A��
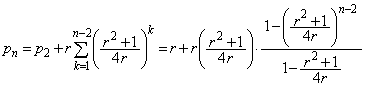
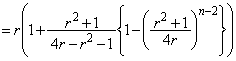 (
(