���l����H���w'11�N�O��[5]
xy���ʏ�ɒ���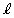 ������B�s��
������B�s��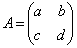 �̕\��1���ϊ�f �́A����(i)�C(ii)�C(iii)�����B
�̕\��1���ϊ�f �́A����(i)�C(ii)�C(iii)�����B
(i) ���ʂ̓_��f �ɂ�鑜�͂��ׂ�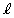 ��ɂ���B
��ɂ���B (ii) f ��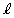 ��̓_�����ׂČ��_�Ɉڂ��B
��̓_�����ׂČ��_�Ɉڂ��B (iii) �_P���~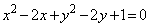 ����Ƃ��Af �ɂ��P�̑���x���W�͍ő�l
����Ƃ��Af �ɂ��P�̑���x���W�͍ő�l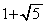 �C�ŏ��l
�C�ŏ��l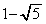 ���Ƃ�B
���Ƃ�B ���̖₢�ɓ�����B
(1) A�����߂�B�܂� �̕����������߂�B
�̕����������߂�B (2) (iii)�ōő�l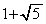 ���Ƃ�Ƃ���P�̍��W�����߂�B
���Ƃ�Ƃ���P�̍��W�����߂�B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@1���ϊ��̊�{���ł��B(i)�C(ii)��A����s��̂Ƃ��ł��������܂��B�ꍇ�������ʓ|�ɂȂ�̂ŁA����(iii)����l�@���܂��傤�B
(1) ����(iii)����l���܂��B�~�̕�������ό`����ƁA
������A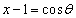 �C
�C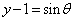 (θ �͔C�ӂ̊p)�Ƃ���(�O�p�����Q��)�ƁA
(θ �͔C�ӂ̊p)�Ƃ���(�O�p�����Q��)�ƁA 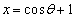 �C
�C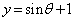 �@����@
�@����@f�@�ɂ��_P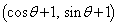 �̑��́A
�̑��́A P�̑���x���WX�́A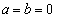 �̏ꍇ(
�̏ꍇ(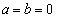 �̏ꍇ�́A
�̏ꍇ�́A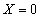 �ƂȂ�A����(iii)�����܂���)�������āA
�ƂȂ�A����(iii)�����܂���)�������āA �A���A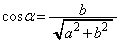 �C
�C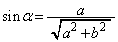 �@����BX�̍ő�l�́A
�@����BX�̍ő�l�́A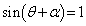 �̂Ƃ��A
�̂Ƃ��A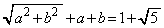 �@����CX�̍ŏ��l�́A
�@����CX�̍ŏ��l�́A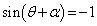 �̂Ƃ��A
�̂Ƃ��A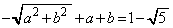 �@����D
�@����D
�C�{�D���A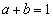 �@����E
�@����E
�C�|�D���A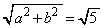
���A
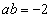 �@����F
�@����F�E�C�F���Aa�Cb�́At��2��������
������A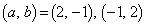 �@����G
�@����G
����(i)���l���܂��B����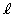 �F
�F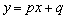 �Ƃ��āA���ʏ�̔C�ӂ̓_
�Ƃ��āA���ʏ�̔C�ӂ̓_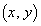 ��f �ɂ�鑜�́A
��f �ɂ�鑜�́A ���ꂪ����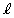 ��ɂ���̂ŁA
��ɂ���̂ŁA ���ʏ�̔C�ӂ̓_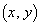 �ɂ��āA���ꂪ�������邽�߂ɁA�P�����̏������A
�ɂ��āA���ꂪ�������邽�߂ɁA�P�����̏������A 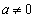 �C
�C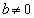 ���A
���A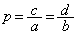 �@����H
�@����H
�܂��A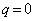 ���A����
���A����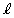 �F
�F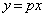 �ƂȂ�܂��B
�ƂȂ�܂��B
����(ii)���l���܂��Bt ��C�ӂ̎����Ƃ��Ē���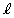 ��̓_
��̓_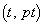 ��f �ɂ�鑜�́A
��f �ɂ�鑜�́A���ꂪ���_�ɂȂ�̂ŁA
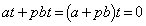 �C
�C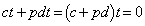
t �͔C�ӂ̎����Ȃ̂ŁA
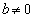 ���
���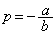 �@����I�@(���ꂪ��������A�H���
�@����I�@(���ꂪ��������A�H���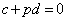 �ƂȂ�܂�)
�ƂȂ�܂�)(a) 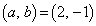 �̂Ƃ��A�I���
�̂Ƃ��A�I���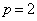 �C�H���A
�C�H���A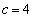 �C
�C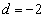 �C����āA
�C����āA (b) 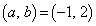 �̂Ƃ��A�I���
�̂Ƃ��A�I���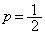 �C�H���A
�C�H���A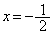 �C
�C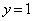 �C����āA
�C����āA
(2) (1)�̇B�ƇG���A
�ƂȂ�܂��B(iii)�ŇA��X���ő�l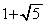 ���Ƃ�Ƃ��A
���Ƃ�Ƃ��A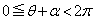 �͈̔͂ōl����ƁA
�͈̔͂ōl����ƁA �ƂȂ�̂ŁA
(a) 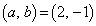 �̂Ƃ��A�@���A
�̂Ƃ��A�@���A (b) 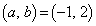 �̂Ƃ��A�@���A
�̂Ƃ��A�@���A
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B 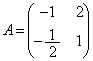 �C
�C