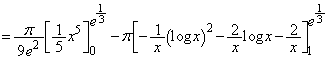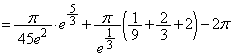���l���嗝�H���w'11�N�O��[4]
xy���ʏ��2�Ȑ�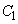 �F
�F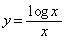 ��
�� �F
�F �͓_P�����L���AP�ɂ����ċ��ʂ̐ڐ��������Ă���B�������Aa�͒萔�Ƃ���B���̖₢�ɓ�����B
�͓_P�����L���AP�ɂ����ċ��ʂ̐ڐ��������Ă���B�������Aa�͒萔�Ƃ���B���̖₢�ɓ�����B
(1) �� �̑����A�ɒl�A�O���t�̉��ʁA�ϋȓ_�ׁA
�̑����A�ɒl�A�O���t�̉��ʁA�ϋȓ_�ׁA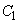 �̊T�`��`���B�������A
�̊T�`��`���B�������A �͏ؖ��Ȃ��ɗp���Ă悢�B
�͏ؖ��Ȃ��ɗp���Ă悢�B (2) P�̍��W�y��a�̒l�����߂�B
(3) �s��ϕ� �����߂�B
�����߂�B (4)  �C
�C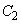 �����x���ň͂܂�镔�����Ax���̂܂���1��]���Ăł��闧�̂̑̐�V�����߂�B
�����x���ň͂܂�镔�����Ax���̂܂���1��]���Ăł��闧�̂̑̐�V�����߂�B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@���ϕ��Ɋւ��鑍�����ł��B
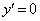 �Ƃ���ƁA
�Ƃ���ƁA �C
�C �C���̂Ƃ��A
�C���̂Ƃ��A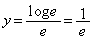
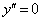 �Ƃ���ƁA
�Ƃ���ƁA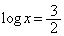 �C
�C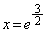 �C���̂Ƃ��A
�C���̂Ƃ��A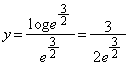 �C�ϋȓ_�́A
�C�ϋȓ_�́A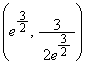 ......[��]�@(���̉������Q��)
......[��]�@(���̉������Q��)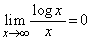 �C
�C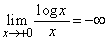 ���A�����\�͈ȉ��̂悤�ɂȂ�܂�(���̑������Q��)�B
���A�����\�͈ȉ��̂悤�ɂȂ�܂�(���̑������Q��)�B| x |
|
| e |
|  |
|
|
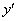 |
| �{ | 0 | �| | �| | �| |
|
 |
| �| | �| | �| | 0 | �{ |
|
| y | ( ) ) |  | 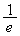 |  | 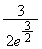 |  | (0) |
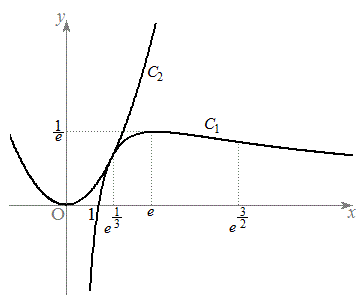 �O���t�͉E�}�B
�O���t�͉E�}�B
(2) �_P��x���W��t �Ƃ���ƁA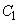 �C
�C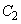 ���_P�����L���邱�Ƃ���A
���_P�����L���邱�Ƃ���A 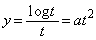 �@����@
�@����@P�ɂ����ċ��ʂ��ڐ��������Ƃ���A �ɂ���
�ɂ��� ���A
���A ��  �@�ɑ�����āA
�@�ɑ�����āA �@���A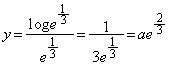 P�̍��W�́A
P�̍��W�́A ......[��]
......[��] 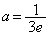 ......[��]
......[��]
(4) ���߂�̐�V�́A(3)�̌��ʂ�p���āA
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B 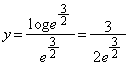 �C�ϋȓ_�́A
�C�ϋȓ_�́A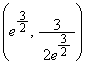 ......[��]�@(���̉������Q��)
......[��]�@(���̉������Q��)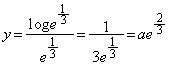
 ......[��]
......[��]