大阪大学理系2021年数学入試問題
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
[1] a,bを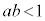 をみたす正の実数とする。xy平面上の点P
をみたす正の実数とする。xy平面上の点P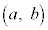 から、曲線
から、曲線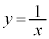 (
(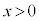 )に2本の接線を引き、その接点をQ
)に2本の接線を引き、その接点をQ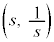 ,R
,R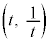 とする。ただし、
とする。ただし、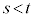 とする。
とする。
(1) sおよびt をa,bを用いて表せ。
(2) 点P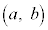 が曲線
が曲線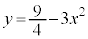 上の
上の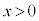 ,
,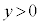 をみたす部分を動くとき、
をみたす部分を動くとき、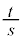 の最小値とそのときのa,bの値を求めよ。
の最小値とそのときのa,bの値を求めよ。 [解答へ]
[2] 空間内に、同一平面上にない4点O,A,B,Cがある。s,tを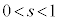 ,
,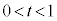 をみたす実数とする。線分OAを1:1に内分する点を
をみたす実数とする。線分OAを1:1に内分する点を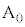 ,線分OBを1:2に内分する点を
,線分OBを1:2に内分する点を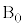 ,線分ACをs:
,線分ACをs: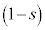 に内分する点をP,線分BCをt :
に内分する点をP,線分BCをt :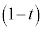 に内分する点をQとする。さらに4点
に内分する点をQとする。さらに4点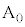 ,
,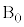 ,P,Qが同一平面上にあるとする。
,P,Qが同一平面上にあるとする。
(1) t をsを用いて表せ。
[解答へ]
[3] nを自然数とし、t を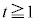 をみたす実数とする。
をみたす実数とする。
(1)  のとき、不等式
のとき、不等式 が成り立つことを示せ。
(2) 不等式
が成り立つことを示せ。
(3) 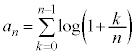 とおく。
とおく。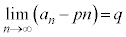 をみたすような実数p,qの値を求めよ。
をみたすような実数p,qの値を求めよ。 [解答へ]
[4] 整数a,b,cに関する次の条件(*)を考える。
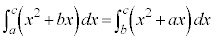 ・・・(*)
・・・(*)(1) 整数a,b,cが(*)および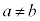 をみたすとき、cは3の倍数であることを示せ。
をみたすとき、cは3の倍数であることを示せ。 (2) 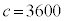 のとき、(*)および
のとき、(*)および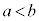 をみたす整数の組
をみたす整数の組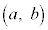 の個数を求めよ。
の個数を求めよ。 [解答へ]
[5] 次の問いに答えよ。
(1) aを実数とする。xについての方程式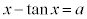 の実数解のうち、
の実数解のうち、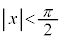 をみたすものがちょうど1個あることを示せ。
をみたすものがちょうど1個あることを示せ。 (2) 自然数nに対し、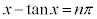 かつ
かつ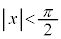 をみたす実数xを
をみたす実数xを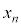 とおく。t を
とおく。t を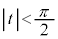 をみたす実数とする。このとき、曲線C:
をみたす実数とする。このとき、曲線C: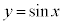 上の点P
上の点P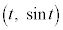 における接線が、不等式
における接線が、不等式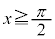 の表す領域に含まれる点においても曲線Cと接するための必要十分条件は、t が
の表す領域に含まれる点においても曲線Cと接するための必要十分条件は、t が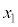 ,
,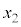 ,
,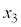 ,・・・のいずれかと等しいことであることを示せ。
,・・・のいずれかと等しいことであることを示せ。 [解答へ]
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
数学TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2024(有)りるらる 苦学楽学塾 随時入会受付中!理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。 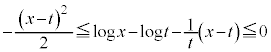
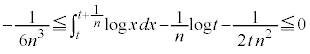
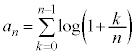 とおく。
とおく。