��嗝�n���w'21�N�O��[3]
n�����R���Ƃ��At ��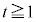 ���݂��������Ƃ���B
���݂��������Ƃ���B
(1) 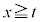 �̂Ƃ��A�s����
�̂Ƃ��A�s���� �����藧���Ƃ������B
(2) �s����
�����藧���Ƃ������B
(3) 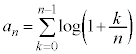 �Ƃ����B
�Ƃ����B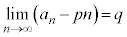 ���݂����悤�Ȏ���p�Cq�̒l�����߂�B
���݂����悤�Ȏ���p�Cq�̒l�����߂�B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@�s����������Ă͂��݂����Ɏ������ނ̂ł����A(3)�����H��2020[5]���v���o��������ł��B
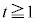 �C
�C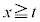 �̂Ƃ��A
�̂Ƃ��A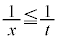 ���A
���A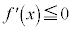 �C����āA
�C����āA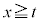 �ɂ����āA
�ɂ����āA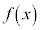 ���P�������ł��B����āA
���P�������ł��B����āA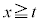 �ɂ����āA
�ɂ����āA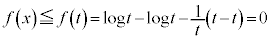 ��
�� 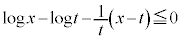 �@����@
�@����@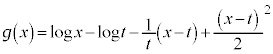 �Ƃ����ƁA
�Ƃ����ƁA����āA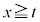 �ɂ����āA
�ɂ����āA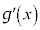 �͒P�������ł��B������A
�͒P�������ł��B������A ����āA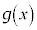 �͒P�������ł��B�]���āA
�͒P�������ł��B�]���āA 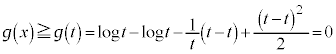 ��
�� 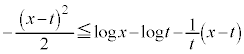 �@����A
�@����A�@�C�A���A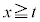 �ɂ����āA
�ɂ����āA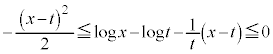
�ȏ���A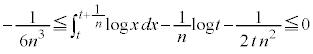
(3) 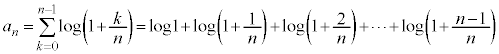 �@����B�@�ł��B
�@����B�@�ł��B �ƂȂ�̂ŁA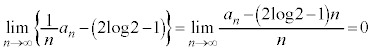 �@����C�@�ł��B
�@����C�@�ł��B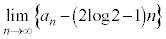 ���L���m��l�Ɏ���(����̋Ɍ����Q��)����·C�͌�����̂ŁA
���L���m��l�Ɏ���(����̋Ɍ����Q��)����·C�͌�����̂ŁA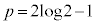 ���낤�Ƃ������ƂɂȂ�܂��B
���낤�Ƃ������ƂɂȂ�܂��B
���āA(2)�̌��ʂŁA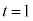 �C
�C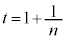 �C
�C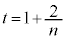 �C����C
�C����C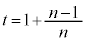 �Ƃ��Ă݂܂��B
�Ƃ��Ă݂܂��B
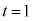 �Ƃ���ƁA
�Ƃ���ƁA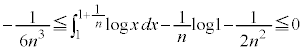
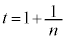 �Ƃ���ƁA
�Ƃ���ƁA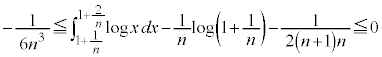
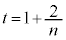 �Ƃ���ƁA
�Ƃ���ƁA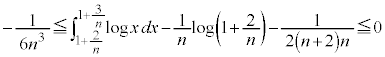
�@�@�@�@�@�@�@�@������
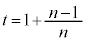 �Ƃ���ƁA
�Ƃ���ƁA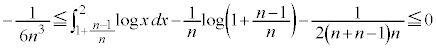
�ӁX�������킹��ƁA �܂��A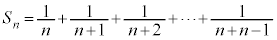 �@����D
�@����D
�Ƃ����ƁA�B��p���āA 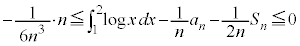 �@����E
�@����E�����ŇD�ɂ��āA
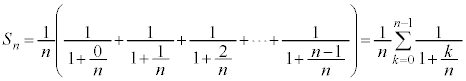
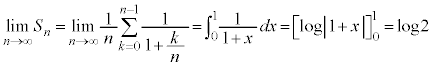 �@����F
�@����F�܂��A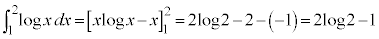 �@����G
�@����G
�E�C�G���A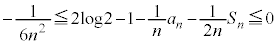
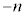 �������āA
�������āA �e�ӂ���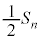 �������ĕό`����ƁA
�������ĕό`����ƁA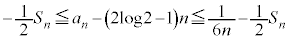
�����ŁA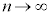 �Ƃ���ƁA�F���A
�Ƃ���ƁA�F���A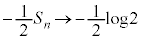 �C
�C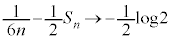 �͂��݂����̌������A
�͂��݂����̌������A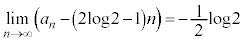
����āA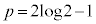 �C
�C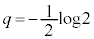 ......[��]
......[��]
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B 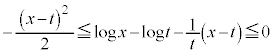
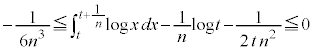
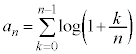 �Ƃ����B
�Ƃ����B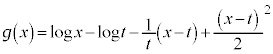 �Ƃ����ƁA
�Ƃ����ƁA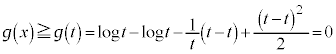
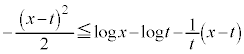 �@����A
�@����A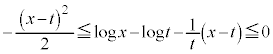
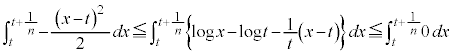
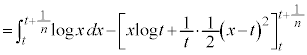
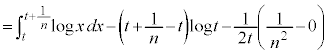
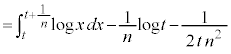
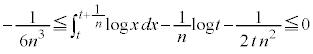
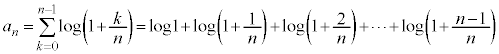 �@����B�@�ł��B
�@����B�@�ł��B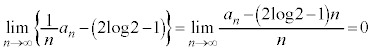 �@����C�@�ł��B
�@����C�@�ł��B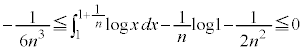
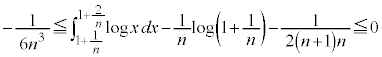
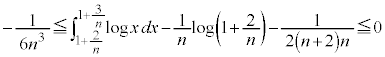
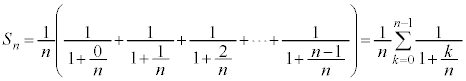
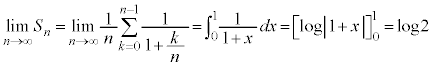 �@����F
�@����F