��嗝�n���w'21�N�O��[5]
���̖₢�ɓ�����B
(1) a�������Ƃ���Bx�ɂ��Ă̕�����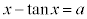 �̎������̂����A
�̎������̂����A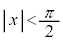 ���݂������̂����傤��1���邱�Ƃ������B
���݂������̂����傤��1���邱�Ƃ������B (2) ���R��n�ɑ��A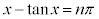 ����
����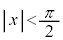 ���݂�������x��
���݂�������x��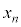 �Ƃ����Bt ��
�Ƃ����Bt ��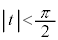 ���݂��������Ƃ���B���̂Ƃ��A�Ȑ�C�F
���݂��������Ƃ���B���̂Ƃ��A�Ȑ�C�F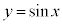 ��̓_P
��̓_P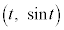 �ɂ�����ڐ����A�s����
�ɂ�����ڐ����A�s����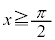 �̕\���̈�Ɋ܂܂��_�ɂ����Ă��Ȑ�C�Ɛڂ��邽�߂̕K�v�\�������́At ��
�̕\���̈�Ɋ܂܂��_�ɂ����Ă��Ȑ�C�Ɛڂ��邽�߂̕K�v�\�������́At ��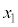 �C
�C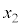 �C
�C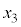 �C����̂����ꂩ�Ɠ��������Ƃł��邱�Ƃ������B
�C����̂����ꂩ�Ɠ��������Ƃł��邱�Ƃ������B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@�K�v�\�������������A�Ƃ������ł����A�u���R��n�ɑ��A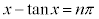 ����
����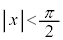 ���݂�������x��
���݂�������x��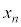 �Ƃ����v��
�Ƃ����v��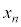 �̒�`�Ȃ̂ŁA
�̒�`�Ȃ̂ŁA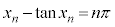 ��O������Ƃ��āA
��O������Ƃ��āA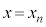 �ɂ�����Ȑ�C�̐ڐ����Ȑ�C��
�ɂ�����Ȑ�C�̐ڐ����Ȑ�C��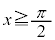 �ɂ����Ă��ړ_�������Ă��āA���A�Ȑ�C��
�ɂ����Ă��ړ_�������Ă��āA���A�Ȑ�C��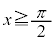 �ɂ�����ڐ���
�ɂ�����ڐ���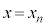 �ɂ����Ă��Ȑ�C�ɐڂ��邱�Ƃ������悤�ɂ��܂��B
�ɂ����Ă��Ȑ�C�ɐڂ��邱�Ƃ������悤�ɂ��܂��B
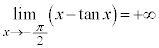 �C
�C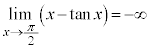 ���A������
���A������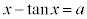 (a�F����)��
(a�F����)��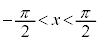 �ɂ����Ă���1�̉�������(���Ԓl�̒藝���Q��)�A��ӂ��������܂��B
�ɂ����Ă���1�̉�������(���Ԓl�̒藝���Q��)�A��ӂ��������܂��B
(2) C�F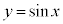 �C��������ƁA
�C��������ƁA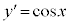 �C
�C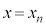 (n�F���R��)�ɂ�����Ȑ�C���ڐ��́A
(n�F���R��)�ɂ�����Ȑ�C���ڐ��́A 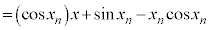 �@����@
�@����@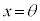 (
(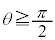 )�ɂ�����Ȑ�C�̐ڐ��́A
)�ɂ�����Ȑ�C�̐ڐ��́A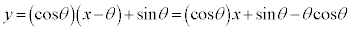 �@����A
�@����A�@�C�A����v���邽�߂ɂ́A
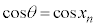 �@����B�@���@
�@����B�@���@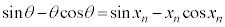 �@����C
�@����C�E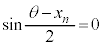 �̂Ƃ��A
�̂Ƃ��A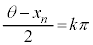 (k�F����)�C
(k�F����)�C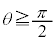 �ɂ����ẮA
�ɂ����ẮA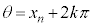 (k�F���R��)
(k�F���R��) ���̂Ƃ��A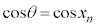 �C
�C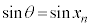 �C�C���A
�C�C���A 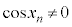 ���A
���A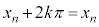 �C����������R��k�Cn�͂���܂���B
�C����������R��k�Cn�͂���܂���B�E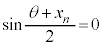 �̂Ƃ��A
�̂Ƃ��A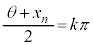 (k�F����)�C
(k�F����)�C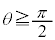 �ɂ����ẮA
�ɂ����ẮA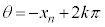 (k�F���R��)�@����D
(k�F���R��)�@����D ���̂Ƃ��A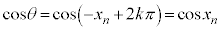 �C
�C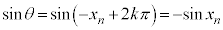 �C�C���A
�C�C���A 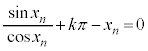 �@��
�@�� 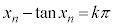
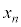 �́A
�́A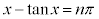 ����
����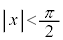 ���݂��������Ȃ̂ŁA
���݂��������Ȃ̂ŁA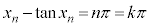 �@��
�@�� 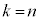
�����A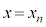 �ɂ�����Ȑ�C�̐ڐ��́A�Ȑ�C��
�ɂ�����Ȑ�C�̐ڐ��́A�Ȑ�C��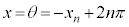 (
(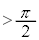 )�ɂ����Ă��ڂ��܂��B
)�ɂ����Ă��ڂ��܂��B ���D���̌��ʂ́A�Ȑ�C�F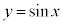 ���A�_
���A�_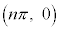 �Ɋւ��ē_�Ώ̂ł��邱�Ƃ���قږ��炩�ŁA�ŏ����炱�̎�����p���ē��Ă��������Ƃ��ł��܂��B
�Ɋւ��ē_�Ώ̂ł��邱�Ƃ���قږ��炩�ŁA�ŏ����炱�̎�����p���ē��Ă��������Ƃ��ł��܂��B �t�ɁA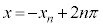 (n�F���R���A
(n�F���R���A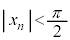 �Ȃ̂ŁA
�Ȃ̂ŁA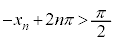
 )�ɂ�����Ȑ�C�̐ڐ��́A
)�ɂ�����Ȑ�C�̐ڐ��́A 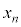 �́A
�́A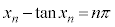 ����
����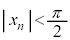 �����̂ŁA
�����̂ŁA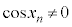 ���A
���A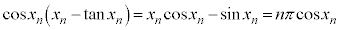 �C�܂�A
�C�܂�A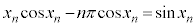 �Ȃ̂ŁA�E�́A
�Ȃ̂ŁA�E�́A�ƂȂ�A�Ȑ�C��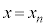 �ɂ�����ڐ��Ɉ�v���܂��B�܂�AC�F
�ɂ�����ڐ��Ɉ�v���܂��B�܂�AC�F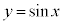 ��̓_P
��̓_P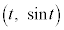 �ɂ�����ڐ����A�s����
�ɂ�����ڐ����A�s����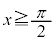 �̕\���̈�Ɋ܂܂��_�ɂ����Ă��Ȑ�C�Ɛڂ���Ƃ��At ��
�̕\���̈�Ɋ܂܂��_�ɂ����Ă��Ȑ�C�Ɛڂ���Ƃ��At ��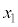 �C
�C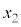 �C
�C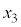 �C����̂����ꂩ�Ɠ������Ȃ�܂��B
�C����̂����ꂩ�Ɠ������Ȃ�܂��B
�ȏ���A�Ȑ�C�F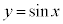 ��̓_P
��̓_P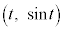 �ɂ�����ڐ����A�s����
�ɂ�����ڐ����A�s����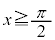 �̕\���̈�Ɋ܂܂��_�ɂ����Ă��Ȑ�C�Ɛڂ��邽�߂��K�v�\�������́At ��
�̕\���̈�Ɋ܂܂��_�ɂ����Ă��Ȑ�C�Ɛڂ��邽�߂��K�v�\�������́At ��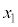 �C
�C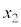 �C
�C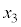 �C����̂����ꂩ�Ɠ��������ƁA�ł��B
�C����̂����ꂩ�Ɠ��������ƁA�ł��B ���D��L�̏ؖ��̍\���́A���̂悤�ɂȂ��Ă��܂��B
�Ȑ�C�� �ɂ�����ڐ��́A
�ɂ�����ڐ��́A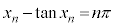 �C
�C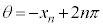 �ł���A�Ȑ�C��
�ł���A�Ȑ�C��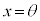 (
(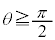 )�ɂ����Ă��ڂ���A�܂�A
)�ɂ����Ă��ڂ���A�܂�A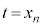 �� �Ȑ�C��
�� �Ȑ�C��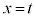 �ɂ�����ڐ��͋Ȑ�C��
�ɂ�����ڐ��͋Ȑ�C��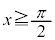 �ɂ����Ă��ڂ���B
�ɂ����Ă��ڂ���B
�܂��A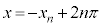 �ɂ�����ڐ����A
�ɂ�����ڐ����A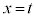 �ɂ�����Ȑ�C�̐ڐ��ƈ�v����Ȃ�
�ɂ�����Ȑ�C�̐ڐ��ƈ�v����Ȃ�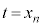 �C�܂�A
�C�܂�A
�Ȑ�C��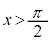 �ɂ�����ڐ���
�ɂ�����ڐ���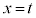 (
(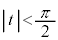 )�ɂ����Ă��ڂ��� ��
)�ɂ����Ă��ڂ��� �� 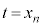
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B  �@��
�@��