��嗝�n���w'21�N�O��[1]
a�Cb��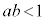 ���݂������̎����Ƃ���Bxy���ʏ�̓_P
���݂������̎����Ƃ���Bxy���ʏ�̓_P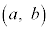 ����A�Ȑ�
����A�Ȑ�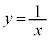 (
(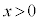 )��2�{�̐ڐ��������A���̐ړ_��Q
)��2�{�̐ڐ��������A���̐ړ_��Q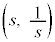 �CR
�CR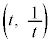 �Ƃ���B�������A
�Ƃ���B�������A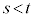 �Ƃ���B
�Ƃ���B
(1) s�����t ��a�Cb��p���ĕ\���B
(2) �_P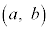 ���Ȑ�
���Ȑ�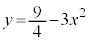 ���
���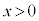 �C
�C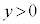 ���݂����������Ƃ��A
���݂����������Ƃ��A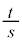 �̍ŏ��l�Ƃ��̂Ƃ���a�Cb�̒l�����߂�B
�̍ŏ��l�Ƃ��̂Ƃ���a�Cb�̒l�����߂�B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@�����ɑ̓����肷��͖̂��d�ł��B
���ꂪ�A�_P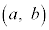 ��ʂ�Ƃ��A
��ʂ�Ƃ��A 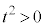 �Ȃ̂ŁA
�Ȃ̂ŁA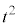 ��������ƁA
��������ƁA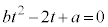 ��
�� 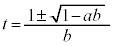
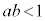 ���A�������͐��ł��B2�ړ_Q�CR��x���W�́A
���A�������͐��ł��B2�ړ_Q�CR��x���W�́A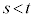 ���A
���A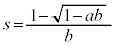 �C
�C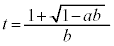 ......[��]
......[��]
(2) �_P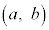 (
(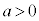 �C
�C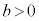 )���Ȑ�
)���Ȑ�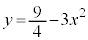 ����̂ŁA
����̂ŁA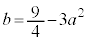 �@����@
�@����@ (1)�̌��ʂ�p���āA
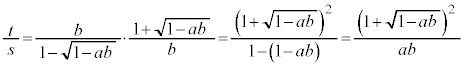 �@����A
�@����A�@���A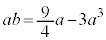 �@����B�@�ƂȂ�̂ŁA
�@����B�@�ƂȂ�̂ŁA �Ƃ��Ă��܂��ƁA������������̂ł́A�v�Z�~�X�̃��X�N���������܂��B�����ŁA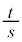 �������Ȃ�a�̊��Ƃ���̂ł͂Ȃ��A����̒i�K�ɕ����邱�Ƃ��l���܂��B�A������ƁA
�������Ȃ�a�̊��Ƃ���̂ł͂Ȃ��A����̒i�K�ɕ����邱�Ƃ��l���܂��B�A������ƁA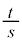 ��
��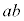 �̊��̌`�ɕ\�������ł��B����ł��悢�̂ł����A���q��2��̌`�����Ă���̂ŁA�����2��̌`�ɂȂ�悤�ɁA
�̊��̌`�ɕ\�������ł��B����ł��悢�̂ł����A���q��2��̌`�����Ă���̂ŁA�����2��̌`�ɂȂ�悤�ɁA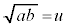 �@����C�@�Ƃ������Ƃɂ��܂��B
�@����C�@�Ƃ������Ƃɂ��܂��B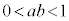 ���A
���A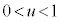 �ł��B�������āA
�ł��B�������āA 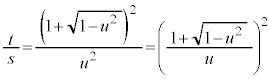 �@����D
�@����D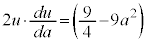 �@��
�@�� 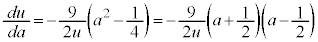
�E�ɑ�����āA
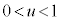 �C
�C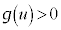 �C
�C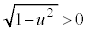 �C
�C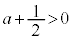 ���A
���A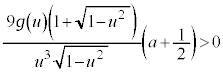 �ƂȂ�̂ŁA�����\�́A�ȉ��̂悤�ɂȂ�܂��B
�ƂȂ�̂ŁA�����\�́A�ȉ��̂悤�ɂȂ�܂��B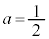 �̂Ƃ��A�@���A
�̂Ƃ��A�@���A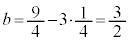 (
(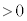 )�C�C���A
)�C�C���A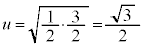 �C�D���A
�C�D���A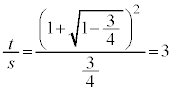 (
(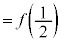 )�����\���A
)�����\���A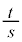 �̍ŏ��l��3�C���̂Ƃ���a�Cb�́A
�̍ŏ��l��3�C���̂Ƃ���a�Cb�́A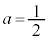 �C
�C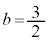 ......[��]
......[��]
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B  �@����A
�@����A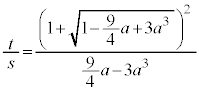
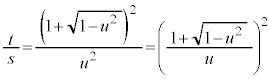 �@����D
�@����D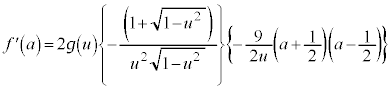
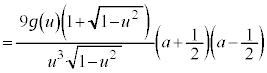
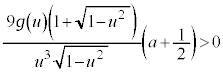 �ƂȂ�̂ŁA�����\�́A�ȉ��̂悤�ɂȂ�܂��B
�ƂȂ�̂ŁA�����\�́A�ȉ��̂悤�ɂȂ�܂��B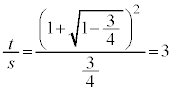 (
(