一橋大学2005年前期数学入試問題
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
[1] kは整数であり、3次方程式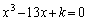
は3つの異なる整数解をもつ。kとこれらの整数解をすべて求めよ。
[解答へ]
[2] 原点を中心とする半径1の円をCとし、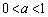
，
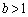とする。
A
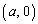とN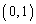
を通る直線がCと交わる点のうちNと異なるものをPとおく。また、B
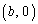とNを通る直線がCと交わる点のうちNと異なるものをQとおく。
(1) Pの座標をaで表せ。
(2) AQ // PBのとき、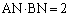
となることを示せ。 (3) AQ // PB，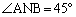
のとき、aの値を求めよ。 [解答へ]
[3]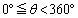 
をみたすθ と正の整数mに対して、
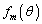を次のように定める。
(1) 
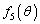を求めよ。 (2) θ が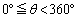
の範囲を動くとき、
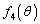の最大値を求めよ。 (3) mがすべての正の整数を動き、θ が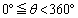
の範囲を動くとき、
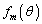の最大値を求めよ。 [解答へ]
[4] aを定数とし、xの2次関数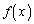
，
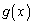を次のように定める。
，
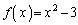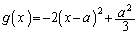
(1) 2つの放物線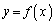
と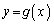
が2つの共有点をもつようなaの範囲を求めよ。 (2) (1)で求めた範囲に属するaの値に対して、2つの放物線によって囲まれる図形を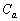
とする。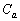
の面積をaで表せ。 (3) aが(1)で求めた範囲を動くとき、少なくとも1つの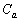
に属する点全体からなる図形の面積を求めよ。 [解答へ]
[5] AとBの2人があるゲームを繰り返し行う。1回ごとのゲームでAがBに勝つ確率はp，BがAに勝つ確率は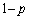
であるとする。n回目のゲームで初めてAとBの双方が4勝以上になる確率を
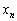とする。
(1) 
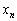をpとnで表せ。
(2) 
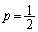のとき、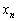
を最大にするnを求めよ。
[解答へ]
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
数学基礎事項TOP 数学TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2024(有)りるらる 苦学楽学塾 随時入会受付中！理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。 