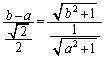�ꋴ�吔�w'05�N�O��[2]
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���_�𒆐S�Ƃ��锼�a1�̉~��C�Ƃ��A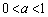 �C
�C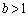 �Ƃ���B
�Ƃ���B
A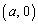 ��N
��N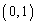 ��ʂ钼����C�ƌ����_�̂���N�ƈقȂ���̂�P�Ƃ����B�܂��AB
��ʂ钼����C�ƌ����_�̂���N�ƈقȂ���̂�P�Ƃ����B�܂��AB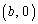 ��N��ʂ钼����C�ƌ����_�̂���N�ƈقȂ���̂�Q�Ƃ����B
��N��ʂ钼����C�ƌ����_�̂���N�ƈقȂ���̂�Q�Ƃ����B
(1) P�̍��W��a�ŕ\���B
(2) AQ // PB�̂Ƃ��A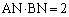 �ƂȂ邱�Ƃ������B
�ƂȂ邱�Ƃ������B (3) AQ // PB�C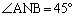 �̂Ƃ��Aa�̒l�����߂�B
�̂Ƃ��Aa�̒l�����߂�B
���@�}�`�ƕ������̌v�Z���ł��B
(3)�͗͐s���ł���Ă��悢�̂ł����A�����ł͏����H�v���Ă݂܂��B
�� 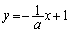 �@����@
�@����@ C�F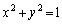 �@����A
�@����A �@�C�A��A�����āA
��������ƁA
����AN�Ɖ~C�Ƃ̌�_�̂���N�ƈقȂ���̂�P�Ȃ̂ŁA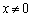 �Ƃ��āA
�Ƃ��āA �@���A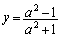
����āAP�̍��W�́A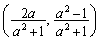 ......[��]
......[��]
(2) B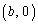 ��N
��N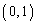 ��ʂ钼���́A�@��a��b�Ɠ���ւ��āA
��ʂ钼���́A�@��a��b�Ɠ���ւ��āA ����ƇA��A������Q�̍��W�����߂�ƁA(1)�̓���a��b�Ɠ���ւ��āA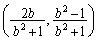
����AQ�̌X���́A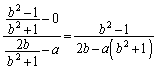 �@(�����̕��������Q��)����BN�̌X���́A
�@(�����̕��������Q��)����BN�̌X���́A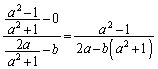 AQ // BN���A�������̌X���͓�����(2�����̕��s�E�������Q��)�A
AQ // BN���A�������̌X���͓�����(2�����̕��s�E�������Q��)�A 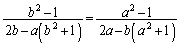 �@����B
�@����B������Đ�������ƁA�B�́Aa��b�����ւ��Ă����藧��(��㎮�ƌ����܂�)�Ȃ̂ŁA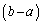 �Ƃ��������������܂��B����ɒ��ӂ��āA
�Ƃ��������������܂��B����ɒ��ӂ��āA 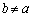 ���A
���A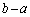 �Ŋ���ƁA
�Ŋ���ƁA�������āA
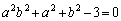 �@����C
�@����C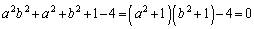
�� 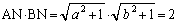
(3) �O�p�`ANB���ʐ�S��2�ʂ�ɕ\�����Ƃ��ł��܂��B(2)�̌��ʂ𗘗p����ƁA ���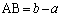 �C����
�C����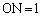 �̎O�p�`�ƌ���ƁA
�̎O�p�`�ƌ���ƁA �� 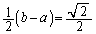
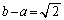 �@����D
�@����D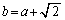 ���C�ɑ�����Ă��悢�̂ł����A4���������ɂȂ��Ă��܂��̂ŁA�C���Ώ̎��ł��邱�Ƃ𗘗p���āA������ƍH�v���܂��B
���C�ɑ�����Ă��悢�̂ł����A4���������ɂȂ��Ă��܂��̂ŁA�C���Ώ̎��ł��邱�Ƃ𗘗p���āA������ƍH�v���܂��B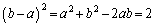 �C
�C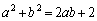 �@����E
�@����E������C�ɑ������ƁA
�� 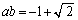 (
(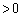 )�E��p���āA
)�E��p���āA �� 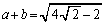 (
(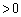 )�@����F
)�@����F
�F�|�D���A 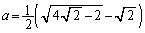 ......[��]
......[��]�ʉ��D�]���藝�������藝���g�����Ƃ��ł��܂��B
�O�p�`ANB�ɗ]���藝��p����ƁA (2)�̌��ʂ�p����ƁA
����ŇD�������܂��B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���w��b����TOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B  �@(�����̕��������Q��)
�@(�����̕��������Q��)