一橋大学2006年前期数学入試問題
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
[1] 次の条件(a)，(b)をともにみたす直角三角形を考える。ただし、斜辺の長さをp、その他の2辺の長さをq，rとする。
(a) p，q，rは自然数で、そのうちの少なくとも2つは素数である。
(b)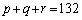 
(1) q，rのどちらかは偶数であることを示せ。
(2) p，q，rの組をすべて求めよ。
[解答へ]
[2] 座標平面上に1辺の長さが2の正三角形ABCがある。ただし、△ABCの重心は原点の位置にあり、辺BCはx軸と平行である。また、頂点Aはy軸上にあってy座標は正であり、頂点Cのx座標は正である。直線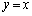
に関して3点A，B，Cと対称な点を、それぞれ
，
，
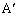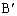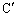とする。
(1) 
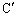の座標を求めよ。 (2) △ABCと△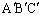
が重なる部分の面積を求めよ。 [解答へ]
[3] 大きさがそれぞれ5，3，1の平面上のベクトル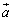
，
，
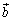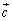に対して、
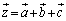とおく。
(1) 
，
，
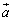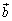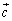を動かすとき、
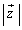の最大値と最小値を求めよ。 (2) 
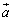を固定し、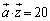
をみたすように
，
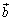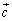を動かすとき、
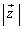の最大値と最小値を求めよ。 [解答へ]
[4] a，bを正の定数とする。関数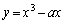
のグラフと、点
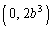を通る直線はちょうど2点P，Qを共有している。ただし、Pのx座標は負、Qのx座標は正である。
(1) 直線PQの方程式をaとbで表せ。
(2) PおよびQの座標をaとbで表せ。
(3) 
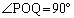となるbが存在するようなaの値の範囲を求めよ。ただし、Oは原点である。 [解答へ]
[5] １，2，3，4が1つずつ記された4枚のカードがある。これらのカードから1枚を抜き出し元に戻すという試行をn回繰り返す。抜き出したn個の数の和を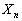
とし、積を
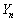とする。
(1) 
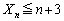となる確率をnで表せ。
(2) 
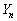が8で割り切れる確率をnで表せ。
[解答へ]
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
数学基礎事項TOP 数学TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2024(有)りるらる 苦学楽学塾 随時入会受付中！理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。