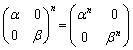�c�嗝�H���w'07�N[A2]
(1) 2�̍s��A��P��
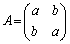 �C
�C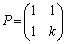
�Ƃ���B�������Aa�Cb�Ck�͂�����������ŁA �ł���AP�͋t�s��
�ł���AP�͋t�s��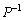 �����Ƃ���B���̂Ƃ��Aα��β �������Ƃ���
�����Ƃ���B���̂Ƃ��Aα��β �������Ƃ��� �ƂȂ�悤�ɒ萔k�̒l���߂�ƁA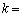 �@�L�@�ł���B�܂��Aα��β ��a��b��p���ĕ\���ƁA
�@�L�@�ł���B�܂��Aα��β ��a��b��p���ĕ\���ƁA �@�N�@�C
�@�N�@�C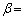 �@�P�@�ƂȂ�B���������āA�s��A��n�̐�
�@�P�@�ƂȂ�B���������āA�s��A��n�̐� ��
�� �Ƃ���ƁAa�Cb�Cn��p���āA �@�R�@�C
�@�R�@�C �@�T�@�ƕ\�����Ƃ��ł���B
�@�T�@�ƕ\�����Ƃ��ł���B (2)  �ł���悤�Ȏ���t�ɑ��A�s��A�ƁA���W���ʏ�̓_
�ł���悤�Ȏ���t�ɑ��A�s��A�ƁA���W���ʏ�̓_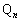
 �C
�C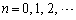 ���A
���A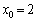 �C
�C �C
�C �ƒ�`����B���̂Ƃ��A���ׂĂ�n�ɂ��� ����t�̒l�͈̔͂�s�����ŕ\���ƁA�@�V�@�ƂȂ�B���̏ꍇ�A
����t�̒l�͈̔͂�s�����ŕ\���ƁA�@�V�@�ƂȂ�B���̏ꍇ�A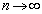 �Ƃ��Ă��_
�Ƃ��Ă��_ �͌��_�ɂ͋߂Â��Ȃ��B
�͌��_�ɂ͋߂Â��Ȃ��B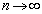 �̂Ƃ��ɓ_
�̂Ƃ��ɓ_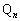 �����_�Ɍ���Ȃ��߂Â��悤��t�̒l�͈̔͂�s�����ŕ\���ƁA�@�X�@�ƂȂ�B
�����_�Ɍ���Ȃ��߂Â��悤��t�̒l�͈̔͂�s�����ŕ\���ƁA�@�X�@�ƂȂ�B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@α�Cβ �́A�s��A���ŗL�l�ŁA�s��A���Ίp�����x�[�X�ɂ������ł����A���䐔��̎�������������߂��v�Z���ɉ߂��܂���B��b�̂������肵�����Ȃ�肪�~�܂�Ƃ���͂���܂���B
���������Ȃ�Ȃ��悤�ɁAα�Cβ�Cγ�Cδ�Ɍ��ʂ������Ă��܂�Ȃ��ŁAα�Cβ�Cγ�Cδ���g���āA�v�Z��i�߂Ă����̂��R�c�ł��B
(1) (�L)�@ �̍�����P���������(�s��̑Ίp�����Q��)�A
�̍�����P���������(�s��̑Ίp�����Q��)�A �܂�A
�� 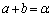 �@����@�C�@
�@����@�C�@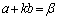 �@����A�C�@
�@����A�C�@ �@����B
�@����B
�A�~k�|�B���A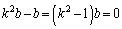
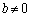 ���A
���A
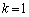 �ł́A
�ł́A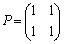 �ƂȂ�A
�ƂȂ�A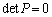 ���A
���A �����݂��Ȃ��Ȃ�̂ŁA
�����݂��Ȃ��Ȃ�̂ŁA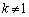 �@(�t�s�����Q��)��
�@(�t�s�����Q��)�� 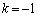
 ......[��]
......[��](�N)�@�@���A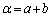
 ......[��]
......[��](�P)�@�A���A
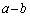 ......[��]
......[��](�R)�@(�L)���A
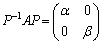 �̗��ӂ�n�悷��ƁA
�̗��ӂ�n�悷��ƁA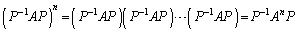 �C
�C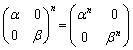
���A
������P�C�E���� �������āA
�������āA (�N)�C(�P)���A
(�T)�@ ......[��]
......[��]
(2) (�V)�@(1)��A�ɂ����āA �C
�C �C
�C �C
�C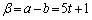 �Ƃ��čl���܂��B
�Ƃ��čl���܂��B ���A
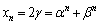 �C
�C
���ׂĂ�n�ɂ��� ���A
���A �� 
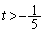 ......[��]
......[��]���̂Ƃ��A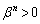 �C
�C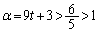 ���A
���A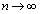 �̂Ƃ��A
�̂Ƃ��A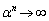 �C
�C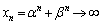 �ƂȂ�A�_
�ƂȂ�A�_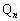
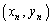 �́A���_�ɋ߂Â��܂���(���䐔��̋Ɍ����Q��)�B
�́A���_�ɋ߂Â��܂���(���䐔��̋Ɍ����Q��)�B (�X)�@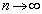 �̂Ƃ��A
�̂Ƃ��A
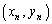 �����_�ɋ߂Â����Ƃ��A
�����_�ɋ߂Â����Ƃ��A ����āA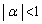 ����
���� 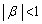 �@(���䐔��̋Ɍ����Q��)��
�@(���䐔��̋Ɍ����Q��)�� 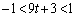 ����
���� 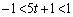 ��
��  ����
���� 
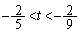 ......[��]
......[��]
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@�c�嗝�H���wTOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B