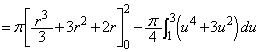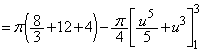�c�嗝�H���w'13�N[4]
������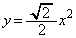 �ƒ���
�ƒ���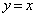 �ň͂܂ꂽ�}�`���A����
�ň͂܂ꂽ�}�`���A����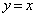 �̂܂���1��]���Ăł��闧�̂̑̐�V�����߂����B
�̂܂���1��]���Ăł��闧�̂̑̐�V�����߂����B
(1) 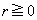 �Ƃ���B����
�Ƃ���B����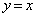 ��ɂ��茴�_O����̋�����r�ƂȂ�_�̂����Ax���W��0�ȏ�̓_��P�Ƃ���B�_P��ʂ蒼��
��ɂ��茴�_O����̋�����r�ƂȂ�_�̂����Ax���W��0�ȏ�̓_��P�Ƃ���B�_P��ʂ蒼��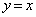 �ɐ����Ȓ�����
�ɐ����Ȓ�����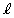 �Ƃ���ƁA
�Ƃ���ƁA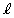 �̕�������
�̕������� �ƂȂ�B�܂��A�_P��������
�ƂȂ�B�܂��A�_P��������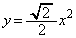 ��ɂ���̂́A
��ɂ���̂́A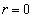 ��
�� �̂Ƃ��ł���B
�̂Ƃ��ł���B (2) 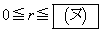 �Ƃ��A�_P�ƒ���
�Ƃ��A�_P�ƒ���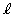 ��(1)�̂悤�ɂƂ�ƁA����
��(1)�̂悤�ɂƂ�ƁA����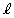 �ƕ�����
�ƕ�����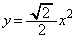 �̌�_�̂����Ax���W��0�ȏ�̓_��Q�Ƃ���B�_P�Ɠ_Q�̋���PQ��2���r��p���ĕ\���ƁA
�̌�_�̂����Ax���W��0�ȏ�̓_��Q�Ƃ���B�_P�Ɠ_Q�̋���PQ��2���r��p���ĕ\���ƁA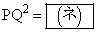 �ƂȂ�B���߂�ߒ�����(2)�ɏ����Ȃ����B
�ƂȂ�B���߂�ߒ�����(2)�ɏ����Ȃ����B (3) ���߂闧�̂̑̐�V��
�ƂȂ邱�Ƃ�p���āAV�����߂Ȃ����B���߂�ߒ�����(3)�ɏ����Ȃ����B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@�Ή�]���̑̐ς����߂���ł��B
(1) ����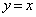 ��ɂ����Č��_O����̋�����r�ƂȂ�_�́AP
��ɂ����Č��_O����̋�����r�ƂȂ�_�́AP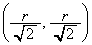 �ł��B
�ł��B 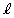 �F
�F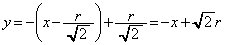 �@����@
�@����@(�j) 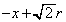 ......[��]
......[��] �� 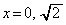 �_P��������
�_P��������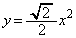 ��ɂ���̂́A
��ɂ���̂́A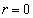 ��
��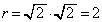 �̂Ƃ��ł��B(�k) 2 ......[��]
�̂Ƃ��ł��B(�k) 2 ......[��]
(2) ������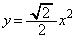 �ƒ���
�ƒ���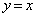 �ň͂܂ꂽ�}�`�́A
�ň͂܂ꂽ�}�`�́A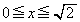 �C�܂�A
�C�܂�A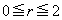 �̕����Ɉʒu���Ă��܂��B
�̕����Ɉʒu���Ă��܂��B �@��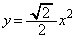 ��A������ƁA
��A������ƁA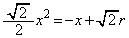
(�l) 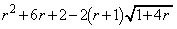 ......[��]
......[��]
(3) ���߂�̐�V�́A 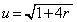 �Ƃ����ƁAr�F
�Ƃ����ƁAr�F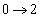 �̂Ƃ��Au�F
�̂Ƃ��Au�F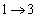
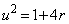 �C
�C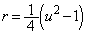 �C
�C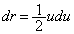 �@(�u���ϕ����Q��)
�@(�u���ϕ����Q��)
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@�c�嗝�H���wTOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B