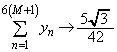�c�嗝�H���w'13�N[5]
z�f���Ƃ���B���R��n�ɑ���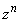 �̎����Ƌ��������ꂼ��
�̎����Ƌ��������ꂼ��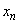 ��
��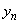 �Ƃ��āA2�̐���
�Ƃ��āA2�̐���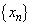 �C
�C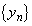 ���l����B�܂�A
���l����B�܂�A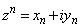 �����Ă���B�����ŁAi�͋����P�ʂł���B
�����Ă���B�����ŁAi�͋����P�ʂł���B
(1) ���f��z���A����θ ��p����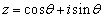 �̌`�ŗ^����ꂽ�Ƃ��A�C�ӂ̎��R��n�ɑ���
�̌`�ŗ^����ꂽ�Ƃ��A�C�ӂ̎��R��n�ɑ���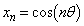 ��
��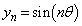 �����藧���Ƃ𐔊w�I�A�[�@��p���ďؖ����Ȃ����B
�����藧���Ƃ𐔊w�I�A�[�@��p���ďؖ����Ȃ����B (2) ���f��z���A���̎���r�Ǝ���θ ��p����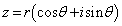 �̌`�ŗ^����ꂽ�Ƃ���B���̂Ƃ��A����
�̌`�ŗ^����ꂽ�Ƃ���B���̂Ƃ��A����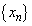 �C
�C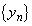 ���Ƃ���0�Ɏ������邽�߂̕K�v�\���������Ar��θ �͈̔͂ŕ\���ƁA
���Ƃ���0�Ɏ������邽�߂̕K�v�\���������Ar��θ �͈̔͂ŕ\���ƁA �ƂȂ�B��(2)�ɁA
�ƂȂ�B��(2)�ɁA �͐���
�͐���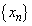 �C
�C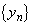 ���Ƃ���0�Ɏ������邽�߂̏\�������ł��邱�ƁA����ѕK�v�����ł��邱�Ƃ̏ؖ��������Ȃ����B
���Ƃ���0�Ɏ������邽�߂̏\�������ł��邱�ƁA����ѕK�v�����ł��邱�Ƃ̏ؖ��������Ȃ����B (3) 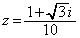 �̂Ƃ��A��������
�̂Ƃ��A��������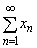 ��
��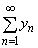 �͂Ƃ��Ɏ������A���ꂼ��̘a��
�͂Ƃ��Ɏ������A���ꂼ��̘a��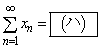 �C
�C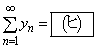 �ł���B
�ł���B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@���Z�͈͂ň������䐔�����������䋉���͎����͈̔͂ōl���܂����A����⏉�������f���ɂȂ�ꍇ�ł����l�̌������������܂��B
�Ȃ��A���f���A�h�E���A�u���̒藝�A�����E�������Q�Ƃ��Ă��������B
(1) 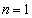 �̂Ƃ��A
�̂Ƃ��A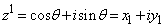 ���A
���A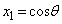 �C
�C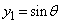 ���A���藧���܂��B
���A���藧���܂��B 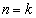 �̂Ƃ��A
�̂Ƃ��A �C
�C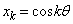 �C
�C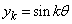 �����藧�Ɖ��肵�܂��B
�����藧�Ɖ��肵�܂��B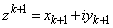 ���A
���A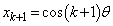 �C
�C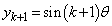
����āA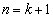 �̂Ƃ��ɂ����藧���܂��B
�̂Ƃ��ɂ����藧���܂��B
����āA���w�I�A�[�@���A�C�ӂ̎��R��n�ɑ��āA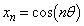 �C
�C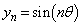 �����藧���܂��B
�����藧���܂��B
(2) 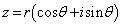 �̂Ƃ��A
�̂Ƃ��A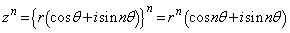
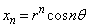 �C
�C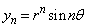
��蕶�̗v���́u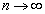 �̂Ƃ��A
�̂Ƃ��A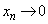 �C
�C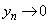 �v�ŁA���̂Ƃ��A
�v�ŁA���̂Ƃ��A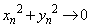 �ƂȂ�͂��ł��B�ł����Aθ �������Ȃ�����ł����Ă��A�C�ӂ̎��R��n�ɑ��āA
�ƂȂ�͂��ł��B�ł����Aθ �������Ȃ�����ł����Ă��A�C�ӂ̎��R��n�ɑ��āA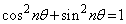 �ƂȂ�̂ŁA
�ƂȂ�̂ŁA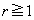 �ł���A
�ł���A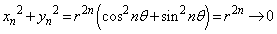 �Ƃ͂Ȃ蓾�܂���B
�Ƃ͂Ȃ蓾�܂���B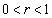 �̂Ƃ��ɂ́A
�̂Ƃ��ɂ́A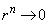 �Ȃ̂ŁA
�Ȃ̂ŁA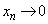 �C
�C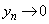 �ƂȂ�܂��B
�ƂȂ�܂��B
����āA����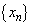 �C
�C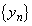 ���Ƃ���0�Ɏ�������(����P)���߂̕K�v�\�������́A
���Ƃ���0�Ɏ�������(����P)���߂̕K�v�\�������́A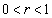 (����Q)�ł��B(�m)
(����Q)�ł��B(�m) 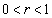 ......[��]
......[��](�\�������ł��邱�ƁFQ �� P)�@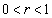 �̂Ƃ��A
�̂Ƃ��A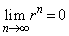 ��
��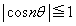 �C
�C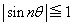 ���A
���A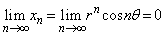 �C
�C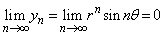
(�K�v�����ł��邱�ƁFP �� Q)�@����u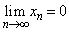 ����
����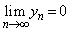 �Ȃ��
�Ȃ��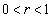 �v�̑�u
�v�̑�u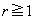 �Ȃ��
�Ȃ��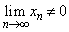 �܂���
�܂���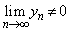 �v�������܂��B
�v�������܂��B 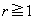 �̂Ƃ��A
�̂Ƃ��A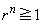 �Ȃ̂ŁA����
�Ȃ̂ŁA����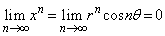 �Ƃ���ƁA
�Ƃ���ƁA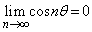 �ƂȂ�܂����A
�ƂȂ�܂����A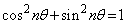 ���A
���A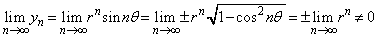 �C����āA���藧�̂ŁA���̖���A�܂�A�K�v�����ł���Ƃ���������������܂��B
�C����āA���藧�̂ŁA���̖���A�܂�A�K�v�����ł���Ƃ���������������܂��B
�Ƃ���ŁA(1)���A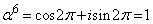 �Ȃ̂ŁA
�Ȃ̂ŁA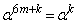 (k�Cm�͎��R���C
(k�Cm�͎��R���C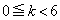 )��p����ƁA
)��p����ƁA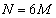 (M�͎��R��)�Ƃ��āA
(M�͎��R��)�Ƃ��āA �����ŁA
�����ŁA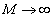 �Ƃ���ƁA
�Ƃ���ƁA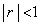 ���A�������䋉���͎������āA
���A�������䋉���͎������āA 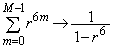 �C
�C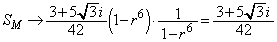 �@����@
�@����@�܂�A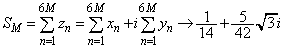 ���A
���A 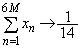 �C
�C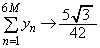
��ʂ̎��R��N�ɂ��Ă��AN��6�Ŋ���������M�Ƃ��āA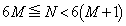 ���A
���A 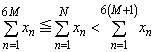 �C
�C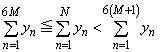 �@����A
�@����A�@�Ɠ��l�ɁA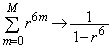 �C
�C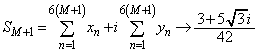 ���A
���A 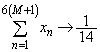 �C
�C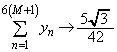
���D��L�ł́A���f���ɂ��ĕs��������邱�Ƃ��ł����A�͂��݂����̌������g���Ȃ��̂ŁA�����Ƌ����ɕ����āA�͂��݂����ɂ��Ă��邱�Ƃɒ��ӂ��Ă��������B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@�c�嗝�H���wTOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B 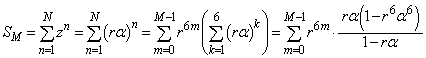
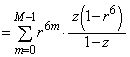
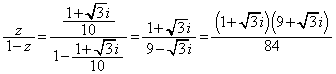
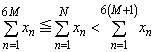 �C
�C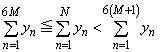 �@����A
�@����A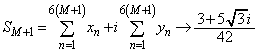 ���A
���A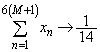 �C
�C