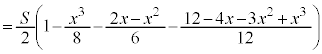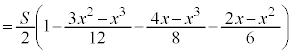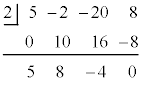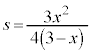�c�嗝�H���w'20�N[5]
���s�l�ӌ`ABCD�ɂ����āA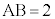 �C
�C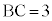 �Ƃ��A�Ίp��AC�̒�����4�Ƃ���B��AB�CBC�CCD�CDA��ɂ��ꂼ��_E�CF�CG�CH��
�Ƃ��A�Ίp��AC�̒�����4�Ƃ���B��AB�CBC�CCD�CDA��ɂ��ꂼ��_E�CF�CG�CH��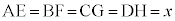 �����悤�ɂƂ�B�������Ax��
�����悤�ɂƂ�B�������Ax��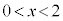 �͈̔͂��Ƃ���B����ɁA�Ίp��AC��ɓ_P��
�͈̔͂��Ƃ���B����ɁA�Ίp��AC��ɓ_P��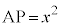 �����悤�ɂƂ�B�ȉ��ł́A���s�l�ӌ`ABCD�̖ʐς�S�Ƃ���B
�����悤�ɂƂ�B�ȉ��ł́A���s�l�ӌ`ABCD�̖ʐς�S�Ƃ���B
(1) ��AEP�̖ʐς�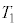 �Ƃ���B
�Ƃ���B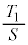 �́Ax��p���ĕ\����
�́Ax��p���ĕ\���� �ƂȂ�B
�ƂȂ�B
(2) ��EFP�̖ʐς�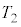 �Ƃ���B
�Ƃ���B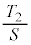 �́A
�́A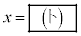 �̂Ƃ��ő�l
�̂Ƃ��ő�l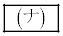 ���Ƃ�B
���Ƃ�B
(3) ��GHP�̖ʐς�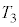 �Ƃ���B
�Ƃ���B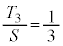 �ƂȂ�̂�
�ƂȂ�̂�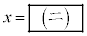 �̂Ƃ��ł���B
�̂Ƃ��ł���B
(4) �_P������EH��ɂ���̂� �̂Ƃ��ł���B
�̂Ƃ��ł���B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@�W���I�Ȍv�Z���ł��B
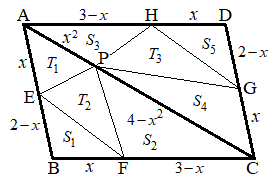 (1)(�e) ��ABC���ʐ��́A
(1)(�e) ��ABC���ʐ��́A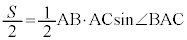 �ł��B������A
�ł��B������A�� 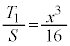 ......[��]
......[��]
(2)(�g) ��BEF�C��CFP���ʐ���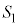 �C
�C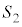 �Ƃ���ƁA(1)�Ɠ��l�ɂ��āA
�Ƃ���ƁA(1)�Ɠ��l�ɂ��āA 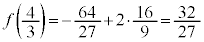 �����\���A
�����\���A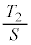 ���ő�ɂȂ�̂́A
���ő�ɂȂ�̂́A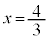 ......[��]�@�̂Ƃ��B
......[��]�@�̂Ƃ��B(�i) �ő�l�́A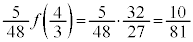 ......[��]
......[��]
(3)(�j) ��AHP�C��CGP�C��DGH�̖ʐς�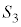 �C
�C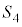 �C
�C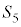 �Ƃ���ƁA
�Ƃ���ƁA 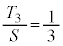 ���A
���A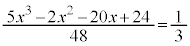
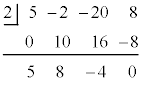 ���Ƃ́A
���Ƃ́A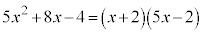 �ƈ����������܂��B
�ƈ����������܂��B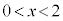 ���A
���A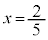 ......[��]
......[��]
P������EH��ɂ���Ƃ��A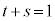 �C
�C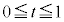 �C
�C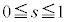 �Ƃ��āA
�Ƃ��āA �A�C�B��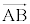 �C
�C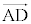 �̌W�����r���āA
�̌W�����r���āA 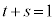 ���A
���A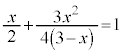
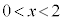 ���A
���A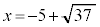 �C���̂Ƃ��A
�C���̂Ƃ��A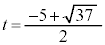 �́A
�́A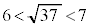 ���A
���A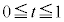 �����̂ŁA
�����̂ŁA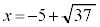 ......[��]
......[��]
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@�c�嗝�H���wTOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B