�c���w���H�w��2024�N���w�������
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
[1](1) 2024�̖̒���1�ԑ傫�����̂�2024�����A6�Ԗڂɑ傫�����̂� �ł���B2024��6�捪�ɍł��߂����R����
�ł���B2024��6�捪�ɍł��߂����R���� �ł���B
�ł���B (2) ��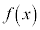 �͎����S�̂Œ�`����Ă���A
�͎����S�̂Œ�`����Ă���A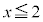 �ɂ�����
�ɂ����� �����Ă�����̂Ƃ���B����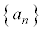 �͑Q����
�͑Q���� �����Ă�����̂Ƃ���B
(i) 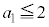 �Ȃ�A���ׂĂ̎��R��n�ɑ���
�Ȃ�A���ׂĂ̎��R��n�ɑ���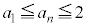 �ƂȂ邱�Ƃ��ؖ����Ȃ����B
�ƂȂ邱�Ƃ��ؖ����Ȃ����B (ii) 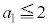 �Ȃ�A
�Ȃ�A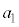 �̒l�ɂ�炸
�̒l�ɂ�炸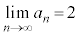 �ƂȂ邱�Ƃ��ؖ����Ȃ����B
�ƂȂ邱�Ƃ��ؖ����Ȃ����B [��]
[2]�@3�̃^�C�v�̃R�C��������B�^�C�v�T�́A���ʂ�H��������Ă���B�^�C�v�U�́A���ʂ�T��������Ă���B�^�C�v�V�́A�Жʂ�H�C�����Жʂ�T��������Ă���B�܂̒��Ƀ^�C�v�T�̃R�C����1���A�^�C�v�U�̃R�C����2���A�^�C�v�V�̃R�C����3�������Ă���B�܂̒�����R�C����1�����o���B
(1) ���o�����R�C���𓊂����Ƃ��AH���o��m���� �ł���B
�ł���B (2) ���o�����R�C���𓊂���H���o���Ƃ��������̉��ŁA���̃R�C�����^�C�v�V�ł�������t���m���� �ł���B
�ł���B (3) ���o�����R�C����2�����Ƃ���2��Ƃ�T���o���Ƃ��������̉��ŁA���̃R�C�����^�C�v�U�ł�������t���m����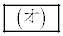 �ł���B
�ł���B (4) ���o�����R�C����2�����Ƃ��A���̌��ʂ���R�C���̃^�C�v��������m���� �ł���B
�ł���B (5) n��2�ȏ�̎��R���Ƃ���B���o�����R�C����n�����Ƃ��A���̌��ʂ���R�C���̃^�C�v��������Ȃ��m���� �ł���B
�ł���B [��]
[3]�@�A����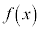 ��
��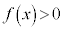 �����A
�����A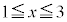 �ŒP���Ɍ���������̂Ƃ���Ba�������Ƃ��AS��
�ŒP���Ɍ���������̂Ƃ���Ba�������Ƃ��AS��
�ƒ�߂�B
(1) 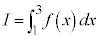 �ƒ�߂�BI��a��p����S��\���ƁA
�ƒ�߂�BI��a��p����S��\���ƁA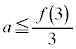 �̂Ƃ�
�̂Ƃ�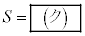 �ƂȂ�A
�ƂȂ�A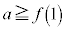 �̂Ƃ�
�̂Ƃ�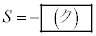 �ƂȂ�B
�ƂȂ�B (2) a��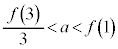 �����Ă���Ƃ��A
�����Ă���Ƃ��A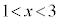 �͈̔͂ŕ�����
�͈̔͂ŕ�����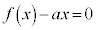 �͉�������1�����Ƃ��ؖ����Ȃ����B
�͉�������1�����Ƃ��ؖ����Ȃ����B (3) a��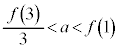 �����Ă���Ƃ���B
�����Ă���Ƃ���B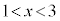 �͈̔͂ɂ��������
�͈̔͂ɂ��������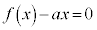 �̉���
�̉���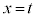 �Ƃ����B���̂Ƃ��Aa����
�Ƃ����B���̂Ƃ��Aa����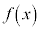 �Ǝ���t ��p���ĕ\����
�Ǝ���t ��p���ĕ\���� �ƂȂ�B�܂��A��
�ƂȂ�B�܂��A��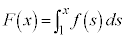 �ƁAt �Ɋւ��镪����
�ƁAt �Ɋւ��镪����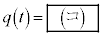 ��p���āA
��p���āA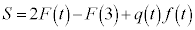 �ƕ\�����B
�ƕ\�����B (4) 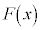 ��(3)�Œ�߂����A
��(3)�Œ�߂����A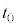 ��
��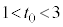 ���������Ƃ���B
���������Ƃ���B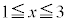 �������ׂĂ̎���x�ɑ�
�������ׂĂ̎���x�ɑ�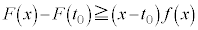 �����藧���Ƃ��ؖ����Ȃ����B
�����藧���Ƃ��ؖ����Ȃ����B (5) 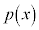 ��
��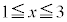 ��
��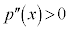 �����������Ƃ��A
�����������Ƃ��A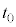 ��
��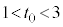 ���������Ƃ���B
���������Ƃ���B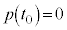 ����
����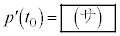 �Ȃ�A
�Ȃ�A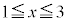 �������ׂĂ̎���x�ɑ�
�������ׂĂ̎���x�ɑ�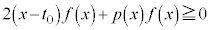 �����藧�B
�����藧�B (6)  �̂Ƃ��ɁAS�͍ŏ��ɂȂ�B
�̂Ƃ��ɁAS�͍ŏ��ɂȂ�B [��]
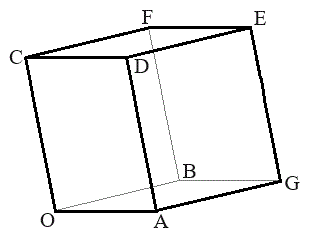 [4]�@���s�Z�ʑ�OAGB-CDEF�ɂ����āA
[4]�@���s�Z�ʑ�OAGB-CDEF�ɂ����āA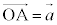 �C
�C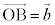 �C
�C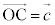 �Ƃ����A
�Ƃ����A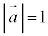 �C
�C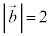 �C
�C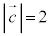 �C
�C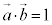 �C
�C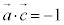 �C
�C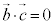 �Ƃ���B
�Ƃ���B(1) �O�p�`OAB�̖ʐς� �ł���B���_C����3�_O�CA�CB��ʂ镽�ʂɐ��������낵�A���̕��ʂƂ̌�_��H�Ƃ���ƁA
�ł���B���_C����3�_O�CA�CB��ʂ镽�ʂɐ��������낵�A���̕��ʂƂ̌�_��H�Ƃ���ƁA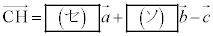 �ł���B�l�ʑ�OABC�̑̐ς�
�ł���B�l�ʑ�OABC�̑̐ς�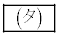 �ł���B
�ł���B
��OA��t�F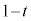 �ɓ�������_��I�C��OB�̒��_��J�C��BF�̒��_��K�Ƃ���B�������A
�ɓ�������_��I�C��OB�̒��_��J�C��BF�̒��_��K�Ƃ���B�������A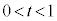 �Ƃ���B
�Ƃ���B
(2) 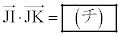 �ł���A�O�p�`IJK�̖ʐς�
�ł���A�O�p�`IJK�̖ʐς�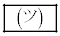 �ł���B
�ł���B (3) 3�_I�CJ�CK��ʂ镽�ʂ���DE�Ƌ��L�_�����̂́A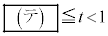 �̂Ƃ��ł���B
�̂Ƃ��ł���B [��]
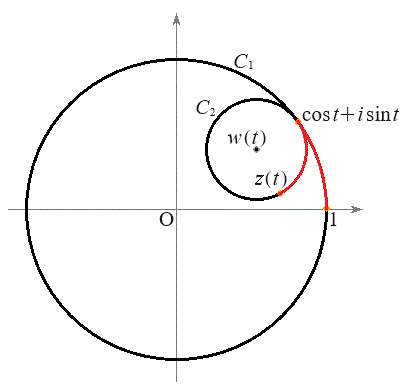 [5]�@���f�����ʏ�ŁA���_O�𒆐S�Ƃ��锼�a1�̉~
[5]�@���f�����ʏ�ŁA���_O�𒆐S�Ƃ��锼�a1�̉~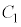 �C�����
�C�����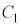 �ɓ��ڂ��锼�ar (
�ɓ��ڂ��锼�ar (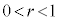 )�̉~
)�̉~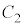 ���l����B
���l����B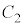 ��ɓ_P���Œ肵�AP�̈ʒu��\�����f����1�ɂȂ�悤��
��ɓ_P���Œ肵�AP�̈ʒu��\�����f����1�ɂȂ�悤��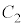 ��z�u����B����
��z�u����B����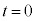 ����
����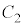 ��
��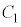 �ɉ����Ă��ׂ邱�ƂȂ���]������B�������A
�ɉ����Ă��ׂ邱�ƂȂ���]������B�������A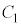 ��
��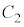 �̐ړ_��
�̐ړ_��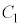 ����v���ɑ���1�ňړ�������̂Ƃ���B���Ȃ킿����
����v���ɑ���1�ňړ�������̂Ƃ���B���Ȃ킿����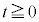 �ɂ�����
�ɂ�����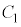 ��
��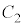 �̐ړ_��\�����f����
�̐ړ_��\�����f����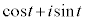 �ł���B
�ł���B(1) P��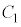 ��Ɉʒu����悤�Ȏ���
��Ɉʒu����悤�Ȏ���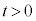 �ōŏ��̂��̂�
�ōŏ��̂��̂�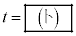 �ł���B
�ł���B (2) ����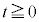 �ɂ�����
�ɂ�����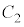 �̒��S��\�����f����
�̒��S��\�����f����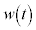 �CP�̈ʒu��\�����f����
�CP�̈ʒu��\�����f����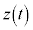 �Ƃ���ƁA
�Ƃ���ƁA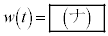 �C
�C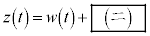 �ł���B
�ł���B (3) ����0���玞��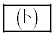 �̊Ԃ�P���������̂��
�̊Ԃ�P���������̂�� �ł���B
�ł���B [��]
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@�c�嗝�H���wTOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B 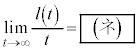 �ł���B
�ł���B