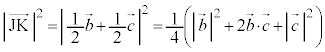�c�嗝�H���w'24�N[4]
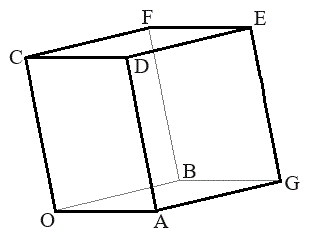 ���s�Z�ʑ�OAGB-CDEF�ɂ����āA
���s�Z�ʑ�OAGB-CDEF�ɂ����āA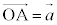 �C
�C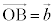 �C
�C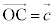 �Ƃ����A
�Ƃ����A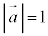 �C
�C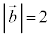 �C
�C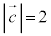 �C
�C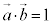 �C
�C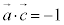 �C
�C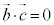 �Ƃ���B
�Ƃ���B
(1) �O�p�`OAB�̖ʐς� �ł���B���_C����3�_O�CA�CB��ʂ镽�ʂɐ��������낵�A���̕��ʂƂ̌�_��H�Ƃ���ƁA
�ł���B���_C����3�_O�CA�CB��ʂ镽�ʂɐ��������낵�A���̕��ʂƂ̌�_��H�Ƃ���ƁA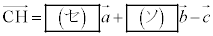 �ł���B�l�ʑ�OABC�̑̐ς�
�ł���B�l�ʑ�OABC�̑̐ς�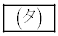 �ł���B
�ł���B
��OA��t�F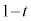 �ɓ�������_��I�C��OB�̒��_��J�C��BF�̒��_��K�Ƃ���B�������A
�ɓ�������_��I�C��OB�̒��_��J�C��BF�̒��_��K�Ƃ���B�������A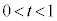 �Ƃ���B
�Ƃ���B
(2) 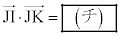 �ł���A�O�p�`IJK�̖ʐς�
�ł���A�O�p�`IJK�̖ʐς�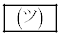 �ł���B
�ł���B (3) 3�_I�CJ�CK��ʂ镽�ʂ���DE�Ƌ��L�_�����̂́A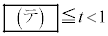 �̂Ƃ��ł���B
�̂Ƃ��ł���B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@�P�Ȃ�v�Z���Ȃ̂ŗ��Ƃ��܂���B
H�́A3�_O�CA�CB��ʂ镽�ʏ�̓_�Ȃ̂ŁAp�Cq�������Ƃ��āA
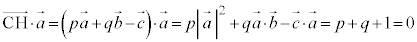 �@����@
�@����@
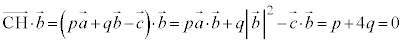 �@����A
�@����A�A�|�@���A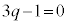 �@��
�@�� 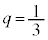 �C
�C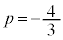
����āA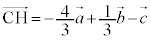 �@
�@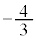 ......[�Z]�@
......[�Z]�@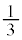 ......[�\]
......[�\] �� 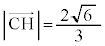 �l�ʑ�OABC���̐��́A
�l�ʑ�OABC���̐��́A 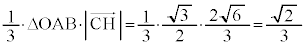 ......[�^]
......[�^]
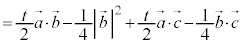
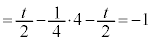 ......[�`]
......[�`]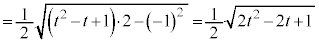 ......[�c]
......[�c]
(3) ��DE��̓_L�́As��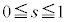 ���������Ƃ��āA
���������Ƃ��āA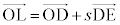 �Ƃ����܂��B
�Ƃ����܂��B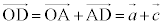 �C
�C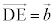 ���A
���A 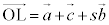 �@����D
�@����D3�_I�CJ�CK��ʂ镽�ʏ�̓_L�́Au�Cv�������Ƃ��āA
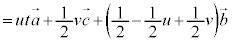 �@����E
�@����E�D�C�E�̌W�����r���āA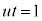 �C
�C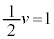 �C
�C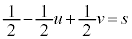
�� 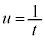 �C
�C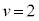 �C
�C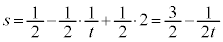
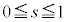 ���A
���A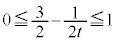 �@��
�@��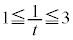
����āA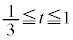 �C��蕶��
�C��蕶��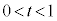 �ƍ��킹�āA
�ƍ��킹�āA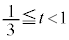 �@
�@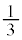 ......[�e]
......[�e]
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@�c�嗝�H���wTOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B