�c�嗝�H���w'24�N[1]
(1) 2024�̖̒���1�ԑ傫�����̂�2024�����A6�Ԗڂɑ傫�����̂� �ł���B2024��6�捪�ɍł��߂����R����
�ł���B2024��6�捪�ɍł��߂����R���� �ł���B
�ł���B (2) ��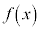 �͎����S�̂Œ�`����Ă���A
�͎����S�̂Œ�`����Ă���A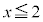 �ɂ�����
�ɂ����� �����Ă�����̂Ƃ���B����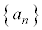 �͑Q����
�͑Q���� �����Ă�����̂Ƃ���B
(i) 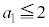 �Ȃ�A���ׂĂ̎��R��n�ɑ���
�Ȃ�A���ׂĂ̎��R��n�ɑ���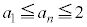 �ƂȂ邱�Ƃ��ؖ����Ȃ����B
�ƂȂ邱�Ƃ��ؖ����Ȃ����B (ii) 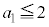 �Ȃ�A
�Ȃ�A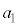 �̒l�ɂ�炸
�̒l�ɂ�炸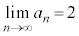 �ƂȂ邱�Ƃ��ؖ����Ȃ����B
�ƂȂ邱�Ƃ��ؖ����Ȃ����B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@(1)�͘r�Â��ł��B(2)�́A���w�I�A�[�@�Ƃ͂��݂����������Ă��܂��B
(1) 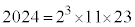 �ł��B���͑S����
�ł��B���͑S����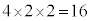 ����A�傫�������珇�ɑS�����ׂ�ƁA2024�C1012�C506�C253�C184�C92�C88�C46�C44�C23�C22�C11�C8�C4�C2�C1�ł��B6�Ԗڂɑ傫�����̂́A92 ......[�A]
����A�傫�������珇�ɑS�����ׂ�ƁA2024�C1012�C506�C253�C184�C92�C88�C46�C44�C23�C22�C11�C8�C4�C2�C1�ł��B6�Ԗڂɑ傫�����̂́A92 ......[�A] 2�悵��2024�ɋ߂����́A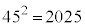 �ł��B3�悵��45�ɋ߂����́A
�ł��B3�悵��45�ɋ߂����́A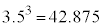 �C
�C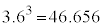
�܂��A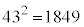 �C����āA
�C����āA �܂�A
����āA2024��6�捪�ɍł��߂����R���́A4 ......[�C]
(2) 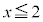 �ɂ����āA
�ɂ����āA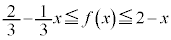 �@����@
�@����@ (i) 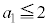 ���A�@��
���A�@��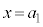 �Ƃ���ƁA
�Ƃ���ƁA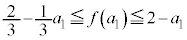 �@����B
�@����B �e�ӂ�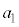 �������āA
�������āA 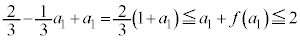 �@����C
�@����C�A�ɂ�����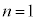 �Ƃ��邱�Ƃɂ��A
�Ƃ��邱�Ƃɂ��A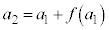 �@����D
�@����D
������C�́A 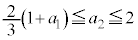 �@����E
�@����E�ƂȂ�܂��B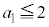 �ƇB���A
�ƇB���A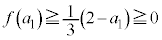
����ƇD����A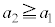
����ƇC�C�D���A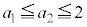 �@����F
�@����F
����ŁA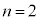 �̏ꍇ�́A�����Ă���̂ŁA
�̏ꍇ�́A�����Ă���̂ŁA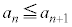 ��
��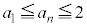 �����w�I�A�[�@�ɂ��ؖ����邱�Ƃ��l���܂��B
�����w�I�A�[�@�ɂ��ؖ����邱�Ƃ��l���܂��B (�T) 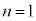 �̂Ƃ��A�F���A
�̂Ƃ��A�F���A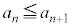 ��
��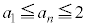 �͐������܂��B
�͐������܂��B (�U) 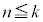 �ƂȂ鎩�R��n�ɂ��āA
�ƂȂ鎩�R��n�ɂ��āA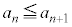 ��
��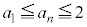 ����������Ɖ��肵�܂��B
����������Ɖ��肵�܂��B �@��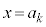 �Ƃ���ƁA
�Ƃ���ƁA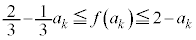 �@����G
�@����G
�e�ӂ�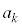 �������āA
�������āA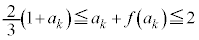
�A���A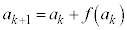
����āA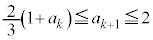 �@����H
�@����H
�G���A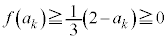 �ƂȂ�̂ŁA
�ƂȂ�̂ŁA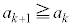 �ł����āA
�ł����āA ����āA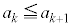 �C
�C
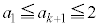 �ƂȂ�A
�ƂȂ�A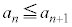 ��
��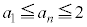 ��
��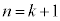 �̂Ƃ����������܂��B
�̂Ƃ����������܂��B (�T)�C(�U)�C���w�I�A�[�@�ɂ��A���ׂĂ̎��R��n�ɂ��āA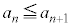 ��
��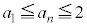 ���������܂��B(�ؖ��I)
���������܂��B(�ؖ��I)
(3) �������A�͂��݂����̌`�����̂ł����A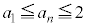 �̂܂܂ł́A
�̂܂܂ł́A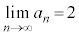 ���܂���B�����ŁA�H�ɒ��ڂ��܂��B(2)���A
���܂���B�����ŁA�H�ɒ��ڂ��܂��B(2)���A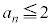 �Ȃ̂ŁA�@�ɂ����āA
�Ȃ̂ŁA�@�ɂ����āA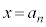 �Ƃ��邱�Ƃɂ��A
�Ƃ��邱�Ƃɂ��A �e�ӂ�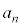 ��������ƁA�A���A
��������ƁA�A���A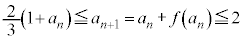 �@����In��
�@����In��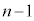 �ɂ������āA
�ɂ������āA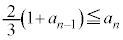
������A ������J��Ԃ��ƁA
�I���A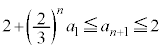
�ԍ���t���ւ��āA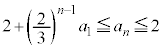
������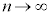 �Ƃ���ƁA
�Ƃ���ƁA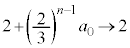
����āA�͂��݂����̌������A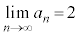 �@(�ؖ��I)
�@(�ؖ��I) �ʉ��D(2)���A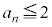 �C�܂��A�I���A
�C�܂��A�I���A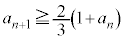
����āA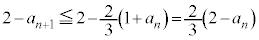
������J��Ԃ��p���邱�Ƃɂ��A �܂�A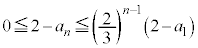
������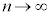 �Ƃ���ƁA
�Ƃ���ƁA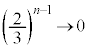 �C�͂��݂����̌������A
�C�͂��݂����̌������A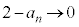
�� 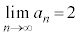
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@�c�嗝�H���wTOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B