�c�嗝�H���w'24�N[3]
�A����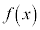 ��
��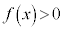 �����A
�����A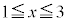 �ŒP���Ɍ���������̂Ƃ���Ba�������Ƃ��AS��
�ŒP���Ɍ���������̂Ƃ���Ba�������Ƃ��AS��
�ƒ�߂�B
(1) 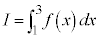 �ƒ�߂�BI��a��p����S��\���ƁA
�ƒ�߂�BI��a��p����S��\���ƁA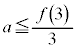 �̂Ƃ�
�̂Ƃ�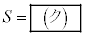 �ƂȂ�A
�ƂȂ�A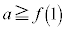 �̂Ƃ�
�̂Ƃ�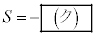 �ƂȂ�B
�ƂȂ�B (2) a��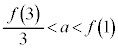 �����Ă���Ƃ��A
�����Ă���Ƃ��A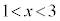 �͈̔͂ŕ�����
�͈̔͂ŕ�����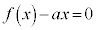 �͉�������1�����Ƃ��ؖ����Ȃ����B
�͉�������1�����Ƃ��ؖ����Ȃ����B (3) a��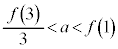 �����Ă���Ƃ���B
�����Ă���Ƃ���B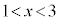 �͈̔͂ɂ��������
�͈̔͂ɂ��������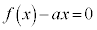 �̉���
�̉���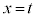 �Ƃ����B���̂Ƃ��Aa����
�Ƃ����B���̂Ƃ��Aa����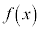 �Ǝ���t ��p���ĕ\����
�Ǝ���t ��p���ĕ\���� �ƂȂ�B�܂��A��
�ƂȂ�B�܂��A��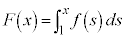 �ƁAt �Ɋւ��镪����
�ƁAt �Ɋւ��镪����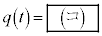 ��p���āA
��p���āA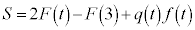 �ƕ\�����B
�ƕ\�����B (4) 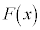 ��(3)�Œ�߂����A
��(3)�Œ�߂����A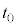 ��
��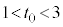 ���������Ƃ���B
���������Ƃ���B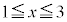 �������ׂĂ̎���x�ɑ�
�������ׂĂ̎���x�ɑ�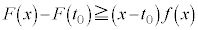 �����藧���Ƃ��ؖ����Ȃ����B
�����藧���Ƃ��ؖ����Ȃ����B (5) 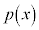 ��
��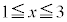 ��
��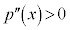 �����������Ƃ��A
�����������Ƃ��A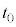 ��
��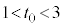 ���������Ƃ���B
���������Ƃ���B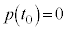 ����
����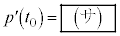 �Ȃ�A
�Ȃ�A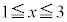 �������ׂĂ̎���x�ɑ�
�������ׂĂ̎���x�ɑ�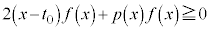 �����藧�B
�����藧�B (6)  �̂Ƃ��ɁAS�͍ŏ��ɂȂ�B
�̂Ƃ��ɁAS�͍ŏ��ɂȂ�B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@��蕶�Ɂu�A����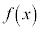 �v�Ƃ���������Ă��Ȃ��̂ŏؖ��͈��J�ł��B(�T)(�V)�́A��[���œ��͂����ɕ�����܂��B�ؖ����l����K�v�͂���܂���B
�v�Ƃ���������Ă��Ȃ��̂ŏؖ��͈��J�ł��B(�T)(�V)�́A��[���œ��͂����ɕ�����܂��B�ؖ����l����K�v�͂���܂���B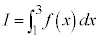 ���o�Ă���̂ŁA�A�����͐ϕ��\�A�Ƃ����O��ōl���܂��傤�B
���o�Ă���̂ŁA�A�����͐ϕ��\�A�Ƃ����O��ōl���܂��傤�B
S�́A��Βl���O���Ă���ϕ��v�Z����̂ł����A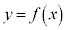 �̃O���t�ƁA���_��ʂ�X��a�̒���
�̃O���t�ƁA���_��ʂ�X��a�̒���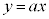 �Ƃ̈ʒu�W�ɂ���ďꍇ�������K�v�ł��B
�Ƃ̈ʒu�W�ɂ���ďꍇ�������K�v�ł��B
�܂��A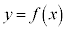 �̃O���t���A2�_
�̃O���t���A2�_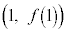 �C
�C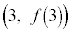 ��ʂ�A����
��ʂ�A����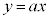 ���A2�_
���A2�_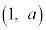 �C
�C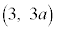 ��ʂ�@���(��)�@���Ƃɒ��ӂ��܂��B
��ʂ�@���(��)�@���Ƃɒ��ӂ��܂��B
�܂��A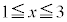 �ɂ�����
�ɂ�����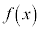 ���A�������P�������A�܂�
���A�������P�������A�܂�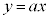 ���A�����P���@���(����)�@�ł��邱�Ƃɒ��ӂ��܂��B
���A�����P���@���(����)�@�ł��邱�Ƃɒ��ӂ��܂��B
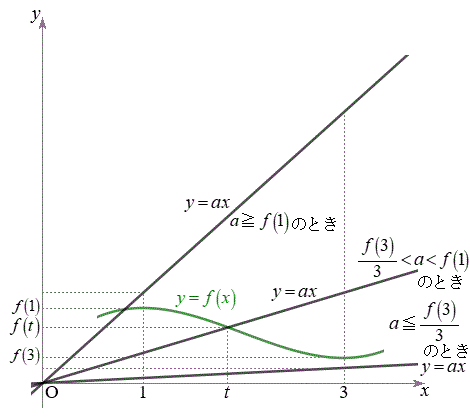 (1)
(1) 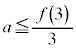 �̂Ƃ��A
�̂Ƃ��A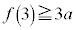 �ł����āA(��)��(����)���A
�ł����āA(��)��(����)���A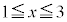 �ɂ�����
�ɂ�����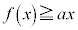 �C
�C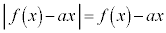 �ł�(��Βl���Q��)�B
�ł�(��Βl���Q��)�B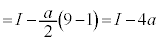 ......[�N]�@����@
......[�N]�@����@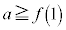 �̂Ƃ��A(��)��(����)���A
�̂Ƃ��A(��)��(����)���A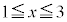 �ɂ�����
�ɂ�����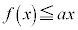 �C
�C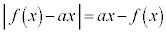 �ł��B
�ł��B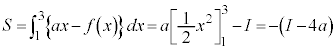 �@����A
�@����A
(2) 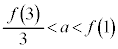 �̂Ƃ��A
�̂Ƃ��A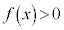 �Ȃ̂�
�Ȃ̂�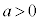 �ł����āA
�ł����āA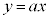 �͒P�������ł��B
�͒P�������ł��B 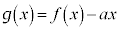 �@����B
�@����B�Ƃ����ƁA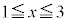 �ɂ����āA(����)���
�ɂ����āA(����)���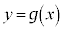 �͘A���Ȍ������ł��B
�͘A���Ȍ������ł��B 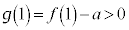 �C
�C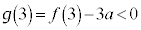
��������Ԓl�̒藝���A������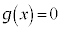 �C����
�C����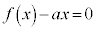 �́A
�́A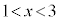 �͈̔͂ɂ���1�̉��������܂��B(�ؖ��I)
�͈̔͂ɂ���1�̉��������܂��B(�ؖ��I)
(3) 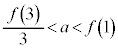 �̂Ƃ��A
�̂Ƃ��A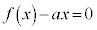 �̉���t �Ƃ���(
�̉���t �Ƃ���(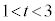 )�ƁA
)�ƁA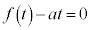 ���A
���A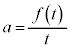 ......[�P]�@����C
......[�P]�@����C 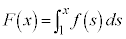 �@����D
�@����D�Ƃ����ƁA
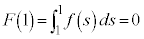 �C
�C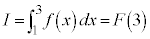 �@����E
�@����E�ł��B
�B��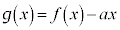 �́A
�́A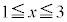 �ɂ����ĒP�������Ȃ̂�
�ɂ����ĒP�������Ȃ̂�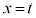 �̑O��ŕ����𐳂��畉�ւƕς��܂��B����āA
�̑O��ŕ����𐳂��畉�ւƕς��܂��B����āA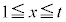 �ɂ�����
�ɂ�����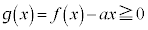 �C
�C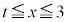 �ɂ�����
�ɂ�����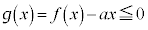
�ϕ���Ԃ�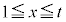 ��
��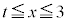 �ɕ����邱�Ƃɂ��A
�ɕ����邱�Ƃɂ��A 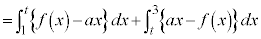
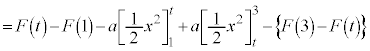 �@(�� �D)
�@(�� �D)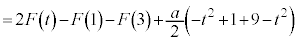
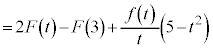 �@(�� �C�C�E)
�@(�� �C�C�E)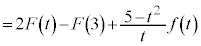 �@����F
�@����F����āA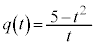 ......[�R]
......[�R]
(4) 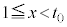 ��
��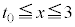 �ɕ����čl���܂��B�ȉ��ŁA�}�`A���}�`B�Ɋ܂܂��A�Ƃ́AA�ɑ����邷�ׂĂ̓_P (
�ɕ����čl���܂��B�ȉ��ŁA�}�`A���}�`B�Ɋ܂܂��A�Ƃ́AA�ɑ����邷�ׂĂ̓_P (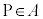 )��B�ɑ�����(
)��B�ɑ�����(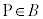 )�A����
)�A����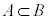 �ł��邱�Ƃ��Ӗ����܂��B
�ł��邱�Ƃ��Ӗ����܂��B 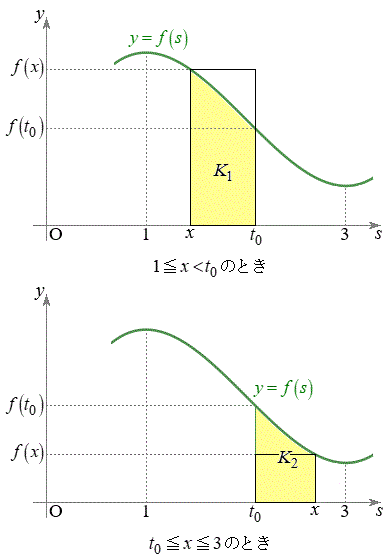 �E
�E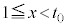 �̂Ƃ��A
�̂Ƃ��A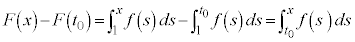 �́A
�́A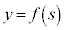 �̃O���t��
�̃O���t��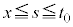 �̕�����s���A����
�̕�����s���A����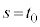 �C����
�C����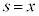 �ň͂܂ꂽ�}�`
�ň͂܂ꂽ�}�`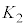 (�E��}�����F���F��)�̖ʐ�
(�E��}�����F���F��)�̖ʐ�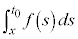 �Ƀ}�C�i�X���������̂ł��B
�Ƀ}�C�i�X���������̂ł��B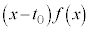 �́A��
�́A��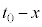 �c
�c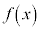 �̒����`
�̒����`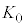 (���F�g)�̖ʐ�
(���F�g)�̖ʐ�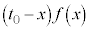 �Ƀ}�C�i�X���������̂ł��B
�Ƀ}�C�i�X���������̂ł��B
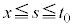 �ɂ�����
�ɂ�����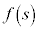 ��s�̘A���Ȍ������Ȃ̂ŁA
��s�̘A���Ȍ������Ȃ̂ŁA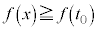 �ł���A�}�`
�ł���A�}�`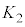 �͒����`
�͒����`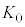 �Ɋ܂܂�܂��B����āA
�Ɋ܂܂�܂��B����āA�� 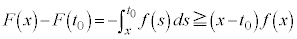
�E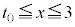 �̂Ƃ��A
�̂Ƃ��A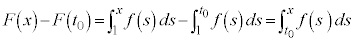 �́A
�́A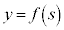 �̃O���t��
�̃O���t��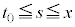 �̕�����s���A����
�̕�����s���A����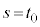 �C����
�C����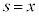 �ň͂܂ꂽ�}�`
�ň͂܂ꂽ�}�`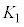 (�E���}�����F���F��)�̖ʐςŁA
(�E���}�����F���F��)�̖ʐςŁA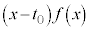 �́A��
�́A��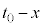 �c
�c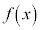 �̒����`
�̒����`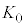 (���F�g)�̖ʐςł��B
(���F�g)�̖ʐςł��B 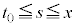 �ɂ�����
�ɂ�����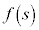 ��s�̘A���Ȍ������Ȃ̂ŁA
��s�̘A���Ȍ������Ȃ̂ŁA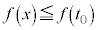 �ł���A�����`
�ł���A�����`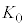 �͐}�`
�͐}�`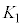 �Ɋ܂܂�܂��B����āA
�Ɋ܂܂�܂��B����āA����āA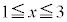 �ɂ����āA
�ɂ����āA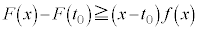 �ł��B(�ؖ��I)
�ł��B(�ؖ��I)
(5) 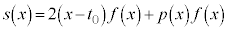 �Ƃ����ƁA
�Ƃ����ƁA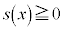 �ƂȂ�悤��
�ƂȂ�悤��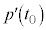 �̒l�����߂�悢�킯�ł��B
�̒l�����߂�悢�킯�ł��B �ƂȂ�̂ŁA
�Ƃ����ƁA
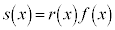 �ł��B�@����G
�ł��B�@����G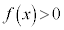 �Ȃ̂ŁA
�Ȃ̂ŁA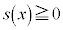 �ł��邽�߂ɂ́A
�ł��邽�߂ɂ́A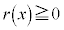 ��������悢�킯�ł��B
��������悢�킯�ł��B
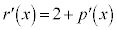 �C
�C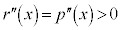 ���A
���A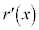 �͒P�������ł��B
�͒P�������ł��B
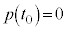 �Ȃ̂ŁA
�Ȃ̂ŁA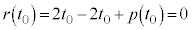 ���A
���A
�ƌ�����A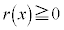 �ƂȂ�܂��B
�ƂȂ�܂��B
���̂��߂ɂ́A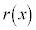 ��
��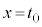 �ŋɏ��ɂȂ�悢�̂ł����A
�ŋɏ��ɂȂ�悢�̂ł����A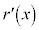 �͒P�������Ȃ̂ŁA
�͒P�������Ȃ̂ŁA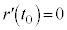 �ł���A
�ł���A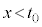 �ɂ�����
�ɂ�����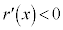 �C
�C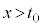 �ɂ�����
�ɂ�����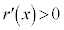 �ƂȂ�̂ŁA
�ƂȂ�̂ŁA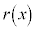 ��
��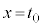 �ɂ����ċɏ��ɂȂ�܂��B���̂��߂ɂ́A
�ɂ����ċɏ��ɂȂ�܂��B���̂��߂ɂ́A 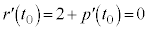 �@��
�@�� 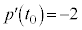 ......[�T]�@����H
......[�T]�@����H�t��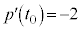 �̂Ƃ��A
�̂Ƃ��A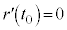 �ł����āA
�ł����āA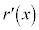 ���P�������ł��邱�Ƃ���A
���P�������ł��邱�Ƃ���A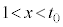 �ł�
�ł�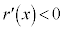 �C
�C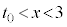 �ɂ����Ă�
�ɂ����Ă�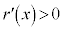
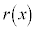 ��
��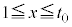 �Ō����A
�Ō����A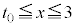 �ő����ł��B
�ő����ł��B
����āA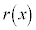 ��
��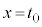 �ɂ����čŏ��l
�ɂ����čŏ��l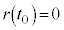 ���Ƃ�A
���Ƃ�A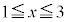 �ɂ�����
�ɂ�����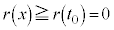 �ł��B
�ł��B
����āA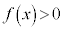 �Ȃ̂ŇG��
�Ȃ̂ŇG��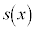 �́A
�́A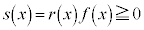 �ł��B�܂�A
�ł��B�܂�A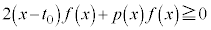 �����藧���܂��B�����œ��������藧�̂́A
�����藧���܂��B�����œ��������藧�̂́A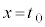 �̂Ƃ��ł��B
�̂Ƃ��ł��B
(6) (1)�@�C�A���A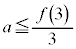 �̂Ƃ�
�̂Ƃ�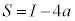 �C
�C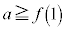 �̂Ƃ�
�̂Ƃ�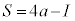 �ł��B�E���
�ł��B�E���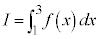 �͒萔�ł��B
�͒萔�ł��B �E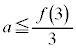 �̂Ƃ�(
�̂Ƃ�(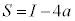 �̂Ƃ����܂�)�A
�̂Ƃ����܂�)�A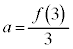 ��a�̌������ŁA
��a�̌������ŁA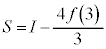 �̂Ƃ��ɁA
�̂Ƃ��ɁA �ŏ��l�F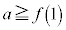 �@����I
�@����I ���Ƃ�܂��B
�E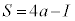 �̂Ƃ��A
�̂Ƃ��A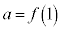 ��a�̑������ŁA
��a�̑������ŁA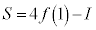 �̂Ƃ��ɁA
�̂Ƃ��ɁA �ŏ��l�F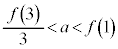 �@����J
�@����J ���Ƃ�܂��B
�E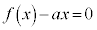 �̂Ƃ��A������
�̂Ƃ��A������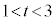 �̉���t (
�̉���t (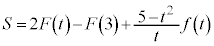 )�Ƃ��āA�F���A
)�Ƃ��āA�F���A 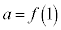 �@����F
�@����F�ƂȂ�܂����A���ɁA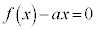 �̂Ƃ��A������
�̂Ƃ��A������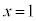 �̉���
�̉���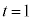 �ŁA
�ŁA
�F��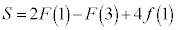 �Ƃ���ƁA
�Ƃ���ƁA 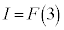 �C
�C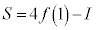 ���A
���A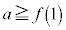 �ƂȂ�A
�ƂȂ�A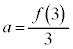 �̂Ƃ��̍ŏ��l�J�Ɉ�v���܂��B
�̂Ƃ��̍ŏ��l�J�Ɉ�v���܂��B
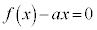 �̂Ƃ��A������
�̂Ƃ��A������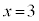 �̉���
�̉���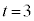 �ŁA�F��
�ŁA�F��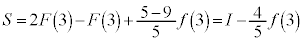 �Ƃ���ƁA
�Ƃ���ƁA�ƂȂ�A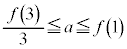 �̂Ƃ��̍ŏ��l�I�Ɉ�v���܂��B
�̂Ƃ��̍ŏ��l�I�Ɉ�v���܂��B
�����ŁA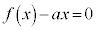 �͈̔͂ŇF��S�̍ŏ��l���l���܂�(����ł��ׂĂ̎���a�ɑ���S�̍ŏ��l���l���邱�ƂɂȂ�܂�)�B���̂Ƃ��A
�͈̔͂ŇF��S�̍ŏ��l���l���܂�(����ł��ׂĂ̎���a�ɑ���S�̍ŏ��l���l���邱�ƂɂȂ�܂�)�B���̂Ƃ��A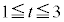 �̉�t �́A
�̉�t �́A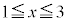 �ł��B(4)���A
�ł��B(4)���A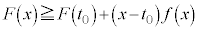 ����x�ɑ��āA
����x�ɑ��āA �F��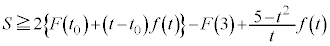 �ɂ����p���āA
�ɂ����p���āA ���̉E�ӂ̂����A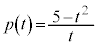 �Ƃ����ƁA(5)�ŁA
�Ƃ����ƁA(5)�ŁA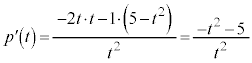 �Ƃ݂āA
�Ƃ݂āA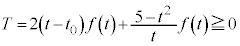 (5)���A
(5)���A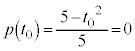 �ƂȂ�̂́A
�ƂȂ�̂́A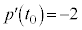 �C
�C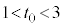 �̂Ƃ�(�H���)�ŁA
�̂Ƃ�(�H���)�ŁA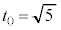 ���
���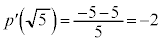 �ŁA���̂Ƃ��m����
�ŁA���̂Ƃ��m����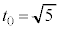 �ƂȂ�܂��B
�ƂȂ�܂��B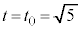 �̂Ƃ��AS�ŏ��ƂȂ�܂����A�C�ɂ�����
�̂Ƃ��AS�ŏ��ƂȂ�܂����A�C�ɂ�����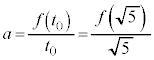 �Ƃ��邱�Ƃɂ��AS���ŏ��Ƃ���a�́A
�Ƃ��邱�Ƃɂ��AS���ŏ��Ƃ���a�́A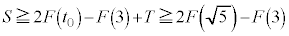 ......[�V]�������āA
......[�V]�������āA 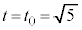 �@(������
�@(������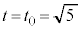 �̂Ƃ�����)
�̂Ƃ�����)
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@�c�嗝�H���wTOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B 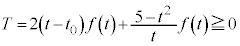
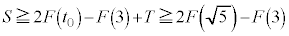 ......[�V]
......[�V]