慶大理工数学'24年[5]
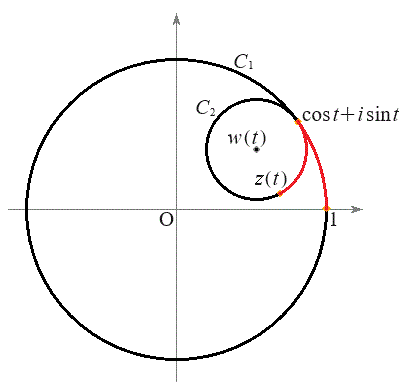 複素数平面上で、原点Oを中心とする半径1の円
複素数平面上で、原点Oを中心とする半径1の円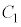 ,および
,および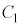 に内接する半径r (
に内接する半径r (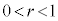 )の円
)の円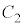 を考える。
を考える。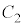 上に点Pを固定し、Pの位置を表す複素数が1になるように
上に点Pを固定し、Pの位置を表す複素数が1になるように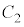 を配置する。時刻
を配置する。時刻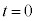 から
から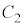 を
を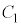 に沿ってすべることなく回転させる。ただし、
に沿ってすべることなく回転させる。ただし、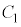 と
と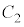 の接点は
の接点は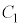 上を反時計回りに速さ1で移動するものとする。すなわち時刻
上を反時計回りに速さ1で移動するものとする。すなわち時刻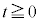 における
における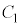 と
と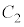 の接点を表す複素数は
の接点を表す複素数は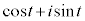 である。
である。
(1) Pが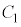 上に位置するような時刻
上に位置するような時刻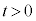 で最小のものは
で最小のものは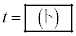 である。
である。 (2) 時刻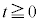 における
における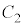 の中心を表す複素数を
の中心を表す複素数を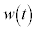 ,Pの位置を表す複素数を
,Pの位置を表す複素数を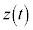 とすると、
とすると、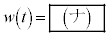 ,
,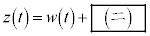 である。
である。 (3) 時刻0から時刻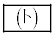 の間にPが動く道のりは
の間にPが動く道のりは である。
である。
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
解答 円の内側を転がる円上の点の軌跡をハイポサイクロイドと言います。ハイポサイクロイドの曲線の長さを求める問題です。
(1) 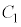 と
と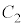 がつねに接するように
がつねに接するように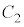 が動くので、最初1にいた
が動くので、最初1にいた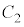 上の点が次に
上の点が次に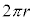 上に位置するまでに接点が
上に位置するまでに接点が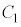 上で移動する長さは
上で移動する長さは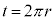 です。
です。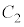 の半径は1なので、速さ1で時間t の間に移動する接点の回転角もt でありそのときの時刻は、
の半径は1なので、速さ1で時間t の間に移動する接点の回転角もt でありそのときの時刻は、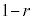 ......[ト]
......[ト] 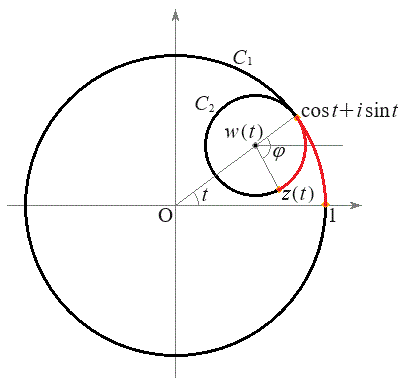
(2) 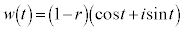 の中心は半径
の中心は半径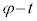 の円周上を動きます。時刻t における
の円周上を動きます。時刻t における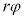 の中心の回転角は接点と同じくt で、
の中心の回転角は接点と同じくt で、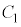 ......[ナ]
......[ナ] Pが円の中心のまわりを原点と接点を結ぶ動径(回転角t )から時計回りに角φ回転しているとして、右図のように実軸方向からの回転角は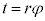 です。Pから接点までの円弧の長さは
です。Pから接点までの円弧の長さは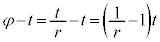 です。これと
です。これと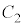 上での接点の移動距離t は等しく、
上での接点の移動距離t は等しく、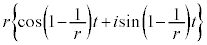
よって、Pの実軸方向からの時計回り(負方向の)の回転角は 反時計回りでの回転角は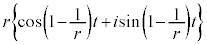 で、Pの
で、Pの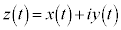 の中心からの変位を表す複素数は、
の中心からの変位を表す複素数は、 つまり、
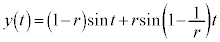
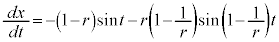 ......[ニ]
......[ニ]
(3) 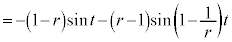 とすると、[ナ]と[ニ]より、
とすると、[ナ]と[ニ]より、 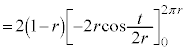 においては、
においては、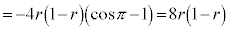 なので、
なので、
(4) (3)の結果によると、nを自然数として、時刻0から時刻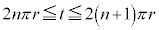 の間にPが動く道のりは、[ヌ]をn倍して
の間にPが動く道のりは、[ヌ]をn倍して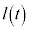 です。
です。 時刻0から時刻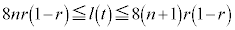 の間にPが動く道のりは
の間にPが動く道のりは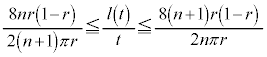 です。
です。
従って、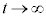 として、時刻0から時刻t の間にPが動く道のり
として、時刻0から時刻t の間にPが動く道のり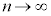 について、
について、 よって、
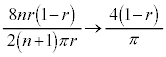 ,
,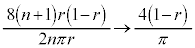
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
慶大理工数学TOP 数学TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2024(有)りるらる 苦学楽学塾 随時入会受付中!理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。 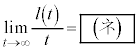 である。
である。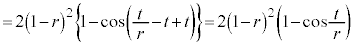
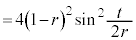
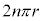
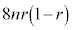
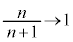
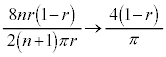 ,
,