���嗝�n���w'22�N�O��[2]
���̒���1����n�܂ł̔ԍ�������n���̎D������B������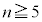 �Ƃ��A�����ԍ��̎D�͂Ȃ��Ƃ���B���̔�����3���̎D���Ɏ��o���A�D�̔ԍ�������������X�CY�CZ�Ƃ���B���̂Ƃ��A
�Ƃ��A�����ԍ��̎D�͂Ȃ��Ƃ���B���̔�����3���̎D���Ɏ��o���A�D�̔ԍ�������������X�CY�CZ�Ƃ���B���̂Ƃ��A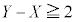 ����
����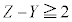 �ƂȂ�m�������߂�B
�ƂȂ�m�������߂�B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@���܂��l����������܂����A�܂������ɂ���Ă݂܂��B
�قȂ�n���̎D����قȂ�3��X�CY�CZ��I�ԑI�ѕ��́A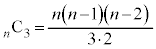 �ʂ�(�g�ݍ��킹���Q��)����A���̊e��ʂ�͓��l�Ɋm���炵���B
�ʂ�(�g�ݍ��킹���Q��)����A���̊e��ʂ�͓��l�Ɋm���炵���B
���̒��ŁA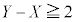 ����
����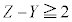 �ƂȂ�Ƃ��A
�ƂȂ�Ƃ��A
X�́A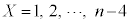 (
(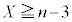 �Ƃ���ƁA
�Ƃ���ƁA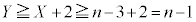 �C
�C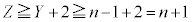 �ƂȂ�
�ƂȂ�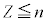 ����Z�����݂��Ȃ��Ȃ�܂�)��
����Z�����݂��Ȃ��Ȃ�܂�)��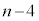 �ʂ肠��܂��BX�����߂�ƁA
�ʂ肠��܂��BX�����߂�ƁA
Y�́A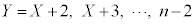 ��
��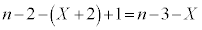 �ʂ肠��܂��BY�����߂�ƁA
�ʂ肠��܂��BY�����߂�ƁA
Z�́A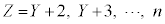 ��
��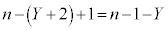 �ʂ肠��܂��B
�ʂ肠��܂��B
����āA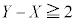 ����
����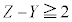 �ƂȂ������(���̌������Q��)�A
�ƂȂ������(���̌������Q��)�A
���߂��m���́A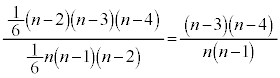 ......[��]
......[��]
�ʉ��D0�ȏ�̐���x�Cy�Cz�ɂ��āA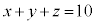 �����������̑g�̌��́A�d���g�ݍ��킹�̍l�����ɂ��ƁA�قȂ�3��ނ���d����������10���ꍇ�̐��ƍl���邱�Ƃɂ��A
�����������̑g�̌��́A�d���g�ݍ��킹�̍l�����ɂ��ƁA�قȂ�3��ނ���d����������10���ꍇ�̐��ƍl���邱�Ƃɂ��A 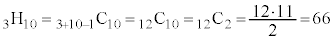 �ʂ�@����A
�ʂ�@����A�Ƃ��ċ��߂邱�Ƃ��ł��܂��B
���̖��̉��p�Ƃ��āA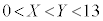 ��������X�CY�̑g�̐����l���Ă݂�ƁA
��������X�CY�̑g�̐����l���Ă݂�ƁA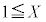 �C
�C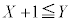 �C
�C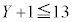 �Ȃ̂ŁA
�Ȃ̂ŁA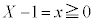 �C
�C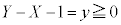 �C
�C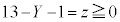 �Ƃ����āA
�Ƃ����āA 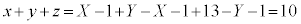 �C�܂�A
�C�܂�A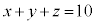
�ƂȂ�0�ȏ�̐����̑g�����߂���ɋA�����A��L�̒ʂ�A66�ʂ�ƂȂ�܂��B
�`���ɏ������u���܂��l�����v�ł����A�{��ł́A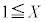 �C
�C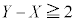 �C
�C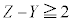 �C
�C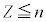 �ƂȂ�̂ŁA
�ƂȂ�̂ŁA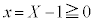 �C
�C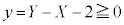 �C
�C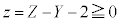 �C
�C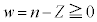 �Ƃ����ƁA
�Ƃ����ƁA 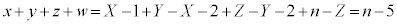 (
(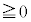 )
)�ƂȂ�̂ŁA�A�Ɠ��l�ɁA�قȂ�4��ނ���d����������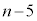 ���g�ݍ��킹�̐��A�ƍl���āA
���g�ݍ��킹�̐��A�ƍl���āA �ƁA�@����C�ɋ��߂邱�Ƃ��ł��܂��B
�Ȃ��A�{��Ƃ͗���܂����A�d���g�ݍ��킹���֗^����m���̖��ŁA���ӂ��Ȃ���Ȃ�Ȃ����Ƃ�����܂��B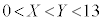 ��������X�CY�̑g�̒��A�܂�A1����12�܂ł̐�������قȂ�2������I�ԂƂ��A
��������X�CY�̑g�̒��A�܂�A1����12�܂ł̐�������قȂ�2������I�ԂƂ��A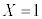 �C
�C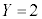 �ƂȂ�m�������߂�ۂɂ́A�S���ۂ̐���
�ƂȂ�m�������߂�ۂɂ́A�S���ۂ̐���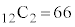 �ʂ�ŁA66�ʂ�͓��l�Ɋm���炵���A�m����
�ʂ�ŁA66�ʂ�͓��l�Ɋm���炵���A�m����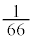 �ƂȂ�܂��B
�ƂȂ�܂��B
�Ƃ��낪�A10�̓��������A�C��B�C��C�ɓ����(�قȂ�3��ނ���d����������10���)�Ƃ��ɁA��A��10���S�ē���m�������߂�A�Ƃ������ł́A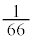 �Ƃł��Ȃ��̂ł��B10�̓��������A�C��B�C��C�ɓ������@�̐���66�ʂ�ł����A66�ʂ�̕��@�̊e1�ʂ肪�A���l�Ɋm���炵���ƌ����Ȃ��A�̂ł��B
�Ƃł��Ȃ��̂ł��B10�̓��������A�C��B�C��C�ɓ������@�̐���66�ʂ�ł����A66�ʂ�̕��@�̊e1�ʂ肪�A���l�Ɋm���炵���ƌ����Ȃ��A�̂ł��B
��A��10���S�ē���ꍇ�ƁA��A��3���A��B��3���A��C��4������ꍇ�Ƃ́A���ꂼ��66�ʂ�̂�����1�ʂ�ł����A���l�Ɋm���炵������܂���B�m���炵�����l����ꍇ�ɂ́A10�����������ł����Ă��A10���ɔԍ������ĈقȂ鋅�Ƃ��čl����K�v������܂��B����ƁA�S���ۂ̐���66�ł͂Ȃ��A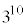 �ł�(�d���������Q��)�B
�ł�(�d���������Q��)�B
��A��10���S�ē���ꍇ�̐���1�ʂ�ł����A��A��3���A��B��3���A��C��4������ꍇ�̐��́A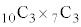 �ʂ�ł��B�]���āA��A��10���S�ē���m����
�ʂ�ł��B�]���āA��A��10���S�ē���m����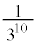 �C��A��3���A��B��3���A��C��4������m���́A
�C��A��3���A��B��3���A��C��4������m���́A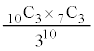 �ł��B
�ł��B
�Q�l���̊m���̖��̉ŁA�u�S���ۂ̊e1�ʂ肪���l�Ɋm���炵���v�ƁA���ǂ��Ǐ����Ă���̂́A���̂��߂ł��B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���嗝�n���wTOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B 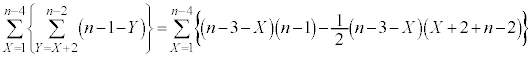
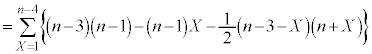
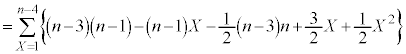
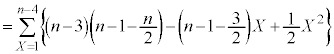
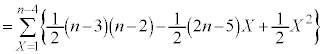
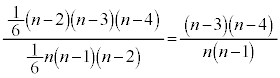 ......[��]
......[��]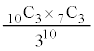 �ł��B
�ł��B