���嗝�n���w'22�N�O��[4]
�l�ʑ�OABC��
�����Ă���Ƃ���BP���BC��̓_�Ƃ��A��OAP�̏d�S��G�Ƃ���B���̂Ƃ��A���̊e��ɓ�����B
(1) 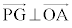 �������B
�������B (2) P����BC����Ƃ��APG�̍ŏ��l�����߂�B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@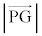 ���l����Ƃ��ɁA��ԃx�N�g���Ƃ��čl����ƁA���όv�Z���ʓ|�Ȃ̂ŁA���ʃx�N�g���Ōv�Z����悤�ɍH�v���܂��B������(1)�𗘗p���邱�ƂɂȂ�܂��B
���l����Ƃ��ɁA��ԃx�N�g���Ƃ��čl����ƁA���όv�Z���ʓ|�Ȃ̂ŁA���ʃx�N�g���Ōv�Z����悤�ɍH�v���܂��B������(1)�𗘗p���邱�ƂɂȂ�܂��B
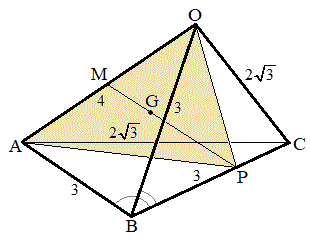
(1) ��ABC�Ɓ�OBC�ɂ����āA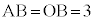 �CBC���ʁA
�CBC���ʁA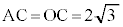
3�ӑ������A��ABC�߁�OBC�C�� ��ABC����OBC����āA��ABP����OBP�C�܂��AAB��OB�CBP���ʁA2�Ӛ�p�������A��ABP�߁�OBP�@�� AP��OP����āA��POA�͓ӎO�p�`PG�̉�����OA�Ƃ̌�_��M�Ƃ���ƁAG�́�OAP�̏d�S�Ȃ̂ŁAM��OA�̒��_�ł��B����āA��PMO����PMA��90���C�����A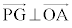
(2) 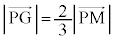 ���
���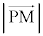 �̍ŏ��l���l���܂��B
�̍ŏ��l���l���܂��B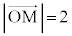 �ƎO�����̒藝���A
�ƎO�����̒藝���A 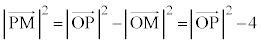 �@����@
�@����@P�͕�BC��̓_�Ȃ̂ŁA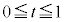 �ƂȂ�t ��p���āA
�ƂȂ�t ��p���āA 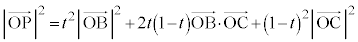 �@����A�@(�������Q��)
�@����A�@(�������Q��)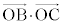 �����߂邽�߂ɁA
�����߂邽�߂ɁA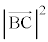 ���l���܂��B
���l���܂��B�܂�A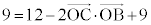 �@��
�@�� 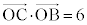 �A���A
�A���A �@���A
����́A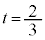 �̂Ƃ��ŏ��l4���Ƃ�܂�(2�����̍ő�E�ŏ����Q��)�B
�̂Ƃ��ŏ��l4���Ƃ�܂�(2�����̍ő�E�ŏ����Q��)�B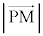 �̍ŏ��l��2�CPG�̍ŏ��l��
�̍ŏ��l��2�CPG�̍ŏ��l��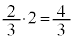 ......[��]
......[��]
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���嗝�n���wTOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B