���嗝�n���w'24�N�O��[3]
���W��Ԃ�4�_O�CA�CB�CC�͓��ꕽ�ʏ�ɂȂ��Ƃ���B����OA�̒��_��P�C����AB�̒��_��Q�Ƃ���B����x�Cy�ɑ��āA����OC��̓_X�ƁA����BC��̓_Y�����̂悤�ɒ�߂�B
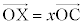 �C
�C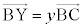
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@����QY�ƒ���PX���˂���̈ʒu�ɂȂ� �� �u����QY�ƒ���PX����_�����A�܂��́AQY // PX�v
����ꊴ�Ȃ̂ł����A�ȉ��ł͂���ʼn��܂����A���Ȃ�ʓ|�ɂȂ�܂��B
�K�v�\�������ɂ��ẮA�����E�������Q�Ƃ��Ă��������B
4�_O�CA�CB�CC�����ꕽ�ʏ�ɂȂ��̂ŁA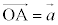 �C
�C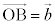 �C
�C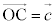 ��1���Ɨ��ł��B�@���(��)
��1���Ɨ��ł��B�@���(��)
�܂��A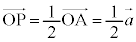 �C
�C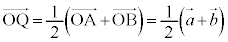 �@����B
�@����B
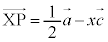 �C
�C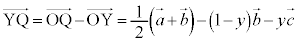 �@����C
�@����C
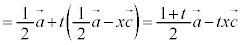 �@����D
�@����D
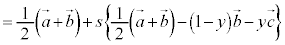
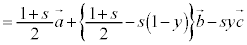 �@����E
�@����E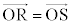 �ƂȂ�s�Ct �����݂��A�D�C�E���A
�ƂȂ�s�Ct �����݂��A�D�C�E���A
(��)���A
�F���A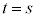
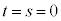 �̏ꍇ�A�G���������Ȃ��Ȃ�̂ŁA
�̏ꍇ�A�G���������Ȃ��Ȃ�̂ŁA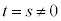 �ł��B
�ł��B
�H���A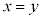
�܂��A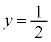 �̂Ƃ��F����s�͑��݂��܂���B
�̂Ƃ��F����s�͑��݂��܂���B
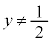 �̂Ƃ�
�̂Ƃ�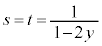 �ƂȂ��_�����݂���̂ŁA��_�����݂��邽�߂ɂ�
�ƂȂ��_�����݂���̂ŁA��_�����݂��邽�߂ɂ�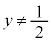 ���K�v�ł��B
���K�v�ł��B
�܂�A����PX�ƒ���QY����_������ �� 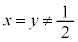
�t�ɁA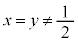 �̂Ƃ��A
�̂Ƃ��A
�D�́A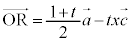
�E�́A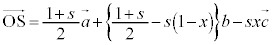
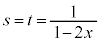 �̂Ƃ��A
�̂Ƃ��A
���A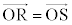 �ƂȂ��_�����݂��܂��B
�ƂȂ��_�����݂��܂��B
����āA����PX�ƒ���QY����_������ �� 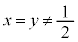 �@����I
�@����I
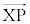 //
//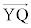 �ƂȂ�Ƃ��A
�ƂȂ�Ƃ��A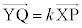 �ƂȂ����k�����݂���̂ŁA�C���A
�ƂȂ����k�����݂���̂ŁA�C���A
(��)���A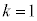 �C
�C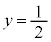 �C
�C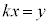
����āA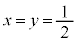 �ł��B
�ł��B
�t��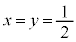 �̂Ƃ��A�C���A
�̂Ƃ��A�C���A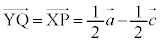 �ƂȂ�A
�ƂȂ�A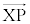 //
//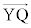 �ƂȂ�܂��B
�ƂȂ�܂��B
����āA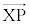 //
//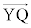 ��
�� 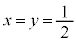 �@����J
�@����J
�I�C�J���A����QY�ƒ���PX���˂���̈ʒu�ɂȂ� �� �u����QY�ƒ���PX����_�����A�܂��́AQY // PX�v �� 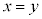
����āA
����QY�ƒ���PX���˂���̈ʒu�ɂ��邽�߂�x�Cy�Ɋւ���K�v�\�������́A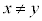 ......[��]
......[��]
[�ʉ�]�@��L�Ŗʓ|�ɂȂ����̂́A����QY�ƒ���PX���˂���̈ʒu�ɂȂ����Ƃ��A��_�����ꍇ�ƕ��s�ɂȂ�ꍇ�ŕ����čl��������ł��B
������܂Ƃ߂čl�����@������܂��B�ŏ����番�����Ă���A�܂Ƃ߂čl���������ǂ��̂ł����A�������ŁA��L�Ŏn�߂Ă��܂����ꍇ�́A���̂܂܉��Ă��܂������ǂ��Ǝv���܂��B
����QY�ƒ���PX���˂���̈ʒu�ɂȂ� �� 4�_P�CQ�CX�CY�����ꕽ�ʏ�ɂ��� �� 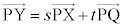 �ƂȂ����s�Ct �����݂���(�x�N�g����1���Ɨ����Q��)�B
�ƂȂ����s�Ct �����݂���(�x�N�g����1���Ɨ����Q��)�B
�@�C�A�C�B���A (��)���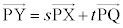 ��
��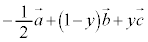 ��1���Ɨ��ł��B�����ŁA
��1���Ɨ��ł��B�����ŁA �Ƃ���ƁA
(��)���A
�K���A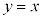
�L���A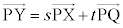
�M���A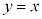
����āA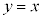 �ƂȂ����s�Ct �����݂��邽�߂ɂ́A
�ƂȂ����s�Ct �����݂��邽�߂ɂ́A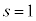
�t��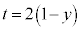 �̂Ƃ��A
�̂Ƃ��A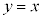 �C
�C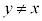 �ƂȂ�s�Ct �����݂���̂ŁA����QY�ƒ���PX�͂˂���̈ʒu�ɂ���܂���B
�ƂȂ�s�Ct �����݂���̂ŁA����QY�ƒ���PX�͂˂���̈ʒu�ɂ���܂���B
�܂�A����QY�ƒ���PX���˂���̈ʒu�ɂȂ� �� 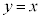 ����āA����QY�ƒ���PX���˂���̈ʒu�ɂ��� ��
����āA����QY�ƒ���PX���˂���̈ʒu�ɂ��� �� 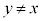
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���嗝�n���wTOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B