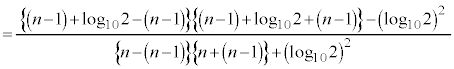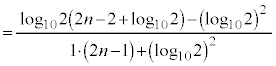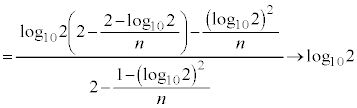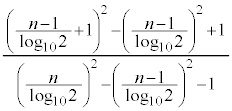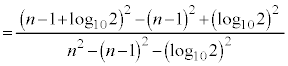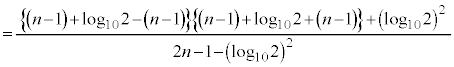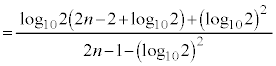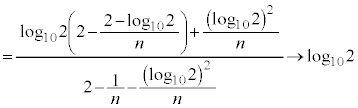���嗝�n���w'24�N�O��[6]
���R��k�ɑ��āA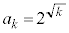 �Ƃ���Bn�����R���Ƃ��A
�Ƃ���Bn�����R���Ƃ��A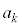 �̐���������n���ł���悤��k�̌���
�̐���������n���ł���悤��k�̌���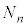 �Ƃ���B�܂��A
�Ƃ���B�܂��A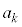 �̐���������n���ł���A���̍ō��ʂ̐�����1�ł���悤��k�̌���
�̐���������n���ł���A���̍ō��ʂ̐�����1�ł���悤��k�̌���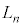 �Ƃ���B�������߂�B
�Ƃ���B�������߂�B
�������A�Ⴆ�Ύ���2345.678�̐�������2345��4���ŁA�ō��ʂ̐�����2�ł���B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@3.9�ȏ�5.1����(5.1�|3.9 = 1.2)�̐����́A4��5��2�ł��B
a�Cb������(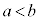 )�Ƃ��āAa�ȏ�b�����̐����̌�M�ɂ��āA
)�Ƃ��āAa�ȏ�b�����̐����̌�M�ɂ��āA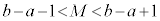 �ł�(�ȉ��̇@�ƇA)�B
�ł�(�ȉ��̇@�ƇA)�B
���������̌�����A�ō��ʂ̐�������p�ΐ���p���čl���܂��B
3���̐���m�́A100�ȏ�1000�����Ȃ̂ŁA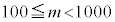 �C�܂�A
�C�܂�A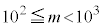 �C��p�ΐ���p���ď����ƁA
�C��p�ΐ���p���ď����ƁA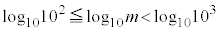 �C�܂�A
�C�܂�A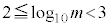 �ł��B
�ł��B
3���̐����ōō��ʂ�1�̐���m�́A100�ȏ�200�����Ȃ̂ŁA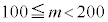 �C�܂�A
�C�܂�A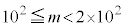 �C��p�ΐ���p���ď����ƁA
�C��p�ΐ���p���ď����ƁA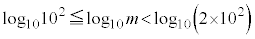 �C�܂�A
�C�܂�A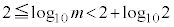 �ł��B
�ł��B
a�Cb�Cc�Cd�𐳐��Ƃ��āA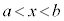 �C
�C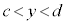 �̂Ƃ��A
�̂Ƃ��A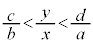 �ł�(�ȉ��̇B)�B
�ł�(�ȉ��̇B)�B
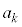 �̐���������n�� ��
�̐���������n�� �� 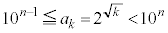 ��
�� 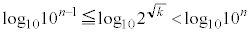 (�ΐ������Q��) ��
(�ΐ������Q��) �� 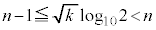 ��
�� 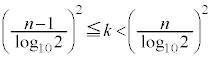
����������R��k�̌�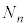 �́A
�́A
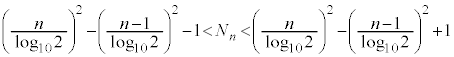 �@����@
�@����@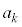 �̐���������n���ł��̍ō��ʂ�1 ��
�̐���������n���ł��̍ō��ʂ�1 �� 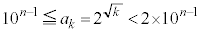 ��
�� 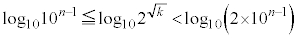 ��
�� 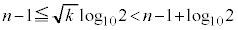 ��
�� 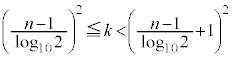
����������R��k�̌�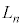 �́A
�́A
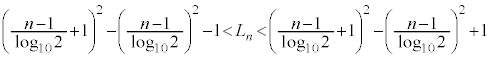 �@����A
�@����A
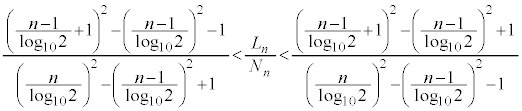 �@����B
�@����B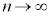 �Ƃ����(����̋Ɍ����Q��)�A
�Ƃ����(����̋Ɍ����Q��)�A
�B�E�ӂ́A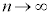 �Ƃ���ƁA
�Ƃ���ƁA
�͂��݂����̌������A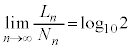 ......[��]
......[��]
���D��L�ł�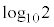 ���������o�Ă��܂��B�������ł͎��Ԑߖ�̂��߁A
���������o�Ă��܂��B�������ł͎��Ԑߖ�̂��߁A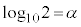 �ƕ����ɂ����ē��Ă������悤�ɂ��܂��傤�B
�ƕ����ɂ����ē��Ă������悤�ɂ��܂��傤�B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���嗝�n���wTOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B 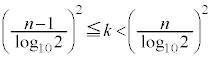
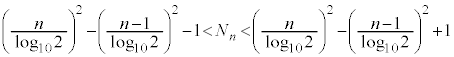 �@����@
�@����@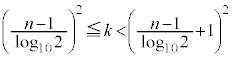
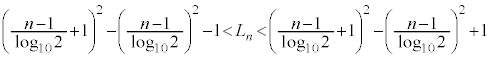 �@����A
�@����A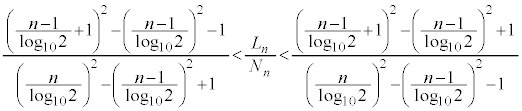 �@����B
�@����B