���嗝�n���w'96�N�O��[5]
xy���ʏ�̐��O�p�`��ABC���l����B��ABC�̏d�S�͌��_O�ɂ���A�x�N�g�� �̒�����1�Ƃ���B��ABC�̓����܂��͕ӏ�̓_
�̒�����1�Ƃ���B��ABC�̓����܂��͕ӏ�̓_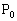 �ɑ��A3���_A�CB�CC����1�_�m��
�ɑ��A3���_A�CB�CC����1�_�m�� �őI�сA���̒��_��
�őI�сA���̒��_�� �̒��_��
�̒��_��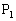 �Ƃ���B���ɓ_
�Ƃ���B���ɓ_ �ɑ��ē��l�̑�����s������ꂽ�_��
�ɑ��ē��l�̑�����s������ꂽ�_��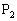 �Ƃ��A�ȉ����̑�����J��Ԃ��āA�_
�Ƃ��A�ȉ����̑�����J��Ԃ��āA�_ �C
�C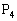 �C����C
�C����C �����B�x�N�g��
�����B�x�N�g��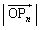 �̒�����2��
�̒�����2�� �̊��Ғl��
�̊��Ғl��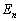 �Ƃ����B
�Ƃ����B
(1)  ���x�N�g��
���x�N�g��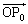 �̒�����p���ĕ\���B
�̒�����p���ĕ\���B (2) �I���_��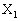 �C
�C �C����C
�C����C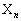 �̂Ƃ��A�x�N�g��
�̂Ƃ��A�x�N�g��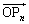 ���x�N�g��
���x�N�g�� ��
�� �C
�C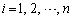 ��p���ĕ\���B
��p���ĕ\���B (3)  �����_O�̂Ƃ�
�����_O�̂Ƃ� �����߂�B
�����߂�B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@���s���w�`���m���ł͔͈͊O�ɂȂ��Ă��܂����A�u�a�̊��Ғl�͊��Ғl�̘a�v�Ƃ����Z�I������t������ł��B
�܂��A�u�a�̊��Ғl�͊��Ғl�̘a�v���ؖ����Ă����܂��B
�ϐ�X��n�ʂ�̒l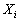 (
(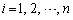 )���Ƃ�A�ϐ�Y��m�ʂ�̒l
)���Ƃ�A�ϐ�Y��m�ʂ�̒l (
( )���Ƃ�Ƃ��܂��B
)���Ƃ�Ƃ��܂��B
�܂��A����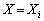 ���N����m��
���N����m�� �C����
�C����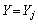 ���N����m��
���N����m��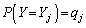 �Ƃ��܂��B
�Ƃ��܂��B
X�CY�����Ғl �C
�C �́A
�́A
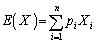 �C
�C
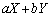 �̊��Ғl���l���Ă݂܂��B
�̊��Ғl���l���Ă݂܂��B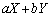 �̂Ƃ肤��l�́A
�̂Ƃ肤��l�́A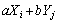 (
(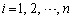 �C
�C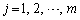 )�ł��B
)�ł��B
���� �ƂȂ�m��
�ƂȂ�m�� �́A
�́A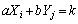 �ƂȂ�i�Cj�̂��ׂĂ̑g�ݍ��킹�ɂ��āA
�ƂȂ�i�Cj�̂��ׂĂ̑g�ݍ��킹�ɂ��āA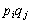 ���������킹�����̂ł��B���̘a��
���������킹�����̂ł��B���̘a��
�Ə������Ƃɂ��܂��Bi�Cj���A �C
�C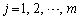 ���Ƃ��A
���Ƃ��A ���Ƃ蓾��l��
���Ƃ蓾��l��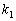 �C
�C �C����C
�C����C (�݂��ɑ��قȂ�)�Ƃ��܂��B
(�݂��ɑ��قȂ�)�Ƃ��܂��B
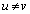 (
(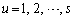 �C
�C )�Ƃ��āA����
)�Ƃ��āA����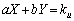 �ƁC����
�ƁC����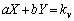 �Ƃ́A�r���ł��B�]���āA
�Ƃ́A�r���ł��B�]���āA �̊��Ғl
�̊��Ғl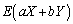 �����߂邽�߂ɁA
�����߂邽�߂ɁA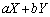 �̂Ƃ肤��l���ׂĂɂ���
�̂Ƃ肤��l���ׂĂɂ��� �̘a���Ƃ�ƁA
�̘a���Ƃ�ƁA
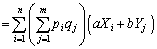 �@(
�@(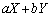 ���Ƃ肤��l���ׂĂɂ킽���Ęa���Ƃ�ƁAX�̂Ƃ肤��l�AY�̂Ƃ肤��l�̂��ׂĂɂ킽���Ęa���Ƃ邱�ƂɂȂ�܂��B�������A�r���Ȃ̂ŁA�d���͂ł��܂���)
���Ƃ肤��l���ׂĂɂ킽���Ęa���Ƃ�ƁAX�̂Ƃ肤��l�AY�̂Ƃ肤��l�̂��ׂĂɂ킽���Ęa���Ƃ邱�ƂɂȂ�܂��B�������A�r���Ȃ̂ŁA�d���͂ł��܂���)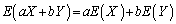
������J��Ԃ��g���An�̕ϐ�������ꍇ�ł��A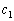 �C
�C �C����C
�C����C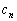 ��萔�Ƃ��āA
��萔�Ƃ��āA
 �@���(��)
�@���(��)
�{��ɖ߂�܂��B
��ӂ��A
(1) 3���_A�CB�CC����1�_��I�ԂƂ��A
(i) A��I�ԂƁA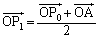
 �@(�� �A)
�@(�� �A)(ii) B��I�ԂƁA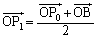
 �@(�� �A)
�@(�� �A) (iii) C��I�ԂƁA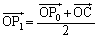
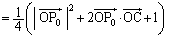 �@(�� �A)
�@(�� �A)����āA

 ......[��]�@(�� �@)
......[��]�@(�� �@)
(2) 
������
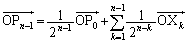 �Ƃ��āA
�Ƃ��āA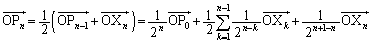
����āA�A�[�I�ɁA
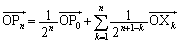 ......[��]
......[��]
(3) (2)�̌��ʂɂ����āA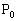 �����_O�̂Ƃ��A
�����_O�̂Ƃ��A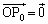 ���A
���A 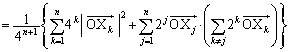 �@(�����ŁA
�@(�����ŁA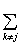 �́Ak���Aj��������1����n�܂œ��������Ƃ��̘a��\�����Ƃɂ��܂�)
�́Ak���Aj��������1����n�܂œ��������Ƃ��̘a��\�����Ƃɂ��܂�)
�����ŁA��L��(��)���g���܂��B�u�a�̊��Ғl�͊��Ғl�̘a�v���A
 �̊��Ғl��
�̊��Ғl��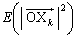 �C
�C �̊��Ғl��
�̊��Ғl�� �Ƃ��āA
�Ƃ��āA  �@����B
�@����B�����ŁA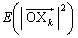 �́A
�́A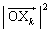 ��
��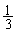 �̊m����
�̊m����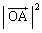 �C
�C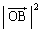 �C
�C ���Ƃ邱�Ƃ���A
���Ƃ邱�Ƃ���A  �@(�� �@)
�@(�� �@)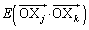 �́A
�́A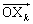 ��
�� �̊m����
�̊m���� �C
�C �C
�C ���Ƃ�A����ƓƗ��ɁA
���Ƃ�A����ƓƗ��ɁA ��
��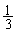 �̊m����
�̊m���� �C
�C �C
�C ���Ƃ邱�Ƃ���A
���Ƃ邱�Ƃ���A����āA�B���A
 ......[��]
......[��]
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���嗝�n���wTOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B 
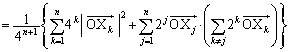 �@(�����ŁA
�@(�����ŁA
 �@����B
�@����B