���H�吔�w'02�N�O��[2]
�ȉ~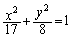 �̊O���̓_P
�̊O���̓_P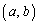 ���������2�{�̐ڐ�����������悤�ȓ_P�̋O�Ղ����߂�B
���������2�{�̐ڐ�����������悤�ȓ_P�̋O�Ղ����߂�B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@���ɂ͂��Ȃ��݂̕p�o�p�^�[�����ł��B
�ȉ~�̕������̕�����ƁA
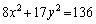 ����@
����@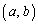 ���������2�{�̐ڐ��́A
���������2�{�̐ڐ��́A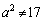 �̏ꍇ�ɂ́A
�̏ꍇ�ɂ́A
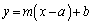 ����A
����A
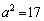 �̏ꍇ�ɂ�2�{�̐ڐ��̕Е���x���ɐ����ɂȂ�̂ł����A���̏ꍇ�ɂ��ẮA�Ō�ɍl���邱�Ƃɂ��܂��B
�̏ꍇ�ɂ�2�{�̐ڐ��̕Е���x���ɐ����ɂȂ�̂ł����A���̏ꍇ�ɂ��ẮA�Ō�ɍl���邱�Ƃɂ��܂��B
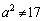 �̏ꍇ�A�A��ό`���āA
�̏ꍇ�A�A��ό`���āA
������@�ɑ�����܂��B�Ȍ�̎��ό`�ł́A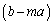 ���ꂭ����ɂ��čs���悤�ɂ��Ă��������B
���ꂭ����ɂ��čs���悤�ɂ��Ă��������B
�W�J���Đ�������ƁA
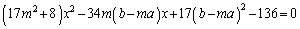 ����B
����B
�W�J���܂��B
��������ƁA
�����m�Ɋւ���2���������ƌ��āA
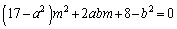 ����C
����C
�ȉ~�ɂ͓_P����2�{�̐ڐ���������̂ł����A����́A2���������C��2�̈قȂ��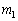 �C
�C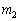 �������Ƃ��Ӗ����Ă��܂��B
�������Ƃ��Ӗ����Ă��܂��B
��ӂł́A����2�{�̐ڐ��͒�������ƌ����Ă��܂��B
2�{�̐ڐ��̌X���͇C�̉��A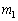 �C
�C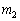 �ł����A��������̂ŁA
�ł����A��������̂ŁA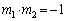 �����藧���܂�(2�����̕��s�E�������Q��)�B
�����藧���܂�(2�����̕��s�E�������Q��)�B
����́A�C��2���̐ς�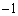 ���ƌ����Ă���킯�ŁA���ƌW���̊W��p���āA
���ƌ����Ă���킯�ŁA���ƌW���̊W��p���āA
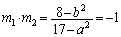 (�����ł�
(�����ł�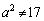 �ł�)
�ł�)
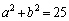 ����D
����D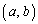 �����_�𒆐S�Ƃ��锼�a5�̉~��C��̓_�ł��邱�Ƃ��Ӗ����Ă��܂��B
�����_�𒆐S�Ƃ��锼�a5�̉~��C��̓_�ł��邱�Ƃ��Ӗ����Ă��܂��B
�͂��߂̕��ŁA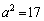 �̏ꍇ��ʈ����ɂ��Ă��܂������A
�̏ꍇ��ʈ����ɂ��Ă��܂������A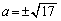 �̂Ƃ��A2�{�̐ڐ��������ɂȂ�̂́A
�̂Ƃ��A2�{�̐ڐ��������ɂȂ�̂́A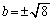 �A�܂�
�A�܂�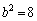 �̂Ƃ��ł��B���̏ꍇ��
�̂Ƃ��ł��B���̏ꍇ��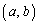 �͇D�����̂ŁA�_P
�͇D�����̂ŁA�_P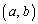 �͉~��C��̓_�ł����āA����ŁA�~��C��̓_�S�ĂɂȂ�܂��B
�͉~��C��̓_�ł����āA����ŁA�~��C��̓_�S�ĂɂȂ�܂��B
�ȏ���A�_P���O���́A���_�𒆐S�Ƃ��锼�a5�̉~�� ......[��]
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���H�吔�wTOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B