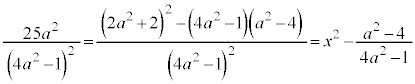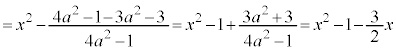���H�吔�w'22�N�O��[4]
a�͐��̎����Ƃ���B���f��z��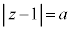 ����
����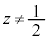 �����Ȃ��瓮���Ƃ��A���f�����ʏ�̓_
�����Ȃ��瓮���Ƃ��A���f�����ʏ�̓_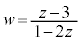 ���`���}�`��K�Ƃ���B���̂Ƃ��A���̖₢�ɓ�����B
���`���}�`��K�Ƃ���B���̂Ƃ��A���̖₢�ɓ�����B
(1) K���~�ƂȂ邽�߂�a�̏��������߂�B�܂��A���̂Ƃ�K�̒��S���\�����f����K�̔��a���A���ꂼ��a��p���ĕ\���B
(2) a��(1)�̏��������Ȃ��瓮���Ƃ��A�����ɕ��s�ʼn~K�̒��a�ƂȂ�������ʉ߂���̈�f�����ʏ�ɐ}������B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@(1)�́A���f���̌v�Z�͖ʓ|�ł������}�ł�(�A�|���j�E�X�̉~���l���Ă��������܂�)�B(2)�͔}��ϐ������ɓ�q���邩���m��܂���B
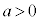 ��z��w�̖��������́A
��z��w�̖��������́A
������@�ɑ������ƁA
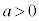 �Ȃ̂ŁA
�Ȃ̂ŁA�����ŁA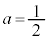 �Ƃ���ƁA
�Ƃ���ƁA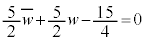 �C
�C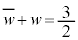
����́Aw�̎�����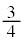 �ł��邱�Ƃ��Ӗ����AK���~�ɂȂ�Ȃ��̂ŁA
�ł��邱�Ƃ��Ӗ����AK���~�ɂȂ�Ȃ��̂ŁA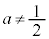 �ł��B�B��
�ł��B�B��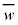 �ɂ��Đ�������ƁA
�ɂ��Đ�������ƁA 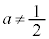 �Ȃ̂ŁA
�Ȃ̂ŁA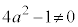 �Ŋ���ƁA
�Ŋ���ƁA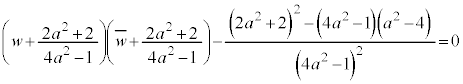 �@����C
�@����C�C����2���̕��q�ɂ��āA
���A�C�́A
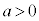 ���A
���A����͉~��\���AK�̕������ł��B����āAK���~�ƂȂ邽�߂̏����́A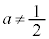 (
(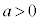 ) ......[��]�~�̒��S�́A
) ......[��]�~�̒��S�́A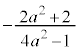 �C���a�́A
�C���a�́A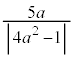 ......[��]
......[��]
(2) �~�̒��S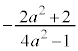 �͎����ŁA�~K�̒��S�͎�����ɂ���̂ŁA�~K�̋����ɕ��s�Ȓ��a�́A�����Ɋւ��đΏ̂ŁA�~�̔��a��
�͎����ŁA�~K�̒��S�͎�����ɂ���̂ŁA�~K�̋����ɕ��s�Ȓ��a�́A�����Ɋւ��đΏ̂ŁA�~�̔��a��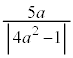 �ł��邱�Ƃ���A���a���[�̋����́A
�ł��邱�Ƃ���A���a���[�̋����́A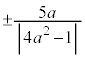 �ł��B���a��̓_�̋���y�́A
�ł��B���a��̓_�̋���y�́A 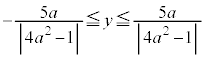
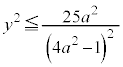 �@����D
�@����D���a�̒��_�A�����~�̒��S�̎����́A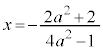 �@����E
�@����E
�D�̉E�ӂ́A�C�̑�2��������ƁA 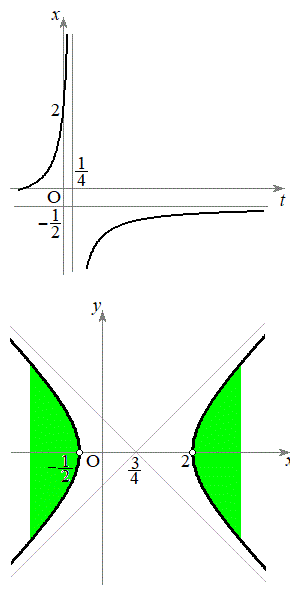 �D���A
�D���A�E�ŁA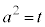 (
(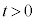 )�Ƃ�����
)�Ƃ�����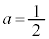 �̂Ƃ�
�̂Ƃ�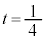 �C
�C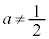 ���
���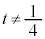 �ł����āA
�ł����āA ���̃O���t��xt���ʏ�ɕ`����(�E��})�A�O���t���A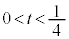 �ɂ����Ă�
�ɂ����Ă�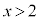 �C
�C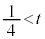 �ɂ����Ă�
�ɂ����Ă�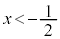
�F�̋��E���F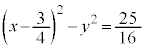 ���o�Ȑ��ł����āA�Q�ߐ���
���o�Ȑ��ł����āA�Q�ߐ���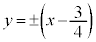 �C�܂��A
�C�܂��A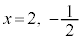 �̂Ƃ�
�̂Ƃ�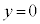
�ȏ��苁�߂�̈�f�����ʏ�ɐ}������ƉE���}���ΐF���F��(���E������܂݁A���}��������)�B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���H�吔�wTOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B 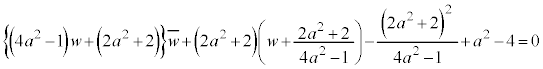
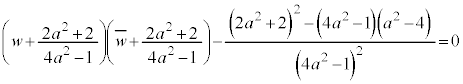 �@����C
�@����C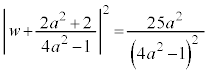
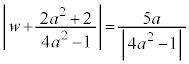
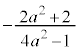 �C���a�́A
�C���a�́A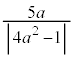 ......[��]
......[��]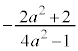 �͎����ŁA�~K�̒��S�͎�����ɂ���̂ŁA�~K�̋����ɕ��s�Ȓ��a�́A�����Ɋւ��đΏ̂ŁA�~�̔��a��
�͎����ŁA�~K�̒��S�͎�����ɂ���̂ŁA�~K�̋����ɕ��s�Ȓ��a�́A�����Ɋւ��đΏ̂ŁA�~�̔��a��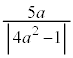 �ł��邱�Ƃ���A���a���[�̋����́A
�ł��邱�Ƃ���A���a���[�̋����́A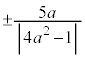 �ł��B���a��̓_�̋���y�́A
�ł��B���a��̓_�̋���y�́A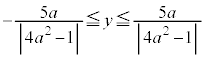
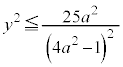 �@����D
�@����D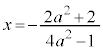 �@����E
�@����E