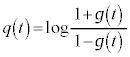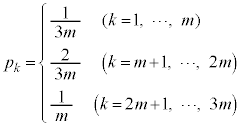東京工業大学2024年前期数学入試問題
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
[1] xy平面上の曲線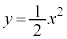 に、点
に、点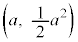 (
(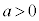 )で接する円のうち、y軸の正の部分にも接するものを
)で接する円のうち、y軸の正の部分にも接するものを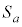 とおく。aが正の実数を動くときの
とおく。aが正の実数を動くときの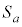 の中心の軌跡をC,とくに
の中心の軌跡をC,とくに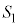 の中心をPとする。
の中心をPとする。 (1) 点Pの座標を求めよ。
(2) 点Pにおける曲線Cの接線の傾きを求めよ。
[解答へ]
[2] 実数全体を定義域にもつ微分可能な関数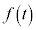 ,
,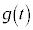 が次の6つの条件を満たしているとする。
が次の6つの条件を満たしているとする。 このとき、
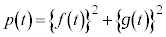 ,
,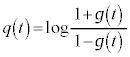
(1) 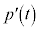 を求めよ。
を求めよ。 (2) 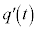 は定数関数であることを示せ。
は定数関数であることを示せ。 (3) 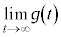 を求めよ。
を求めよ。 (4) 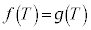 となる正の実数Tに対して、媒介変数表示された平面曲線
となる正の実数Tに対して、媒介変数表示された平面曲線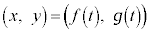 (
(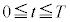 )の長さを求めよ。
)の長さを求めよ。 [解答へ]
[3] xy平面上に、点A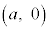 ,B
,B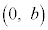 ,C
,C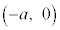 (ただし
(ただし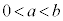 )をとる。点A,Bを通る直線を
)をとる。点A,Bを通る直線を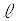 とし、点Cを通り線分BCに垂直な直線をkとする。さらに、点Aを通りy軸に平行な直線と直線kとの交点を
とし、点Cを通り線分BCに垂直な直線をkとする。さらに、点Aを通りy軸に平行な直線と直線kとの交点を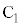 とし、点
とし、点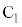 を通りx軸に平行な直線と直線
を通りx軸に平行な直線と直線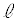 との交点を
との交点を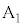 とする。以下、
とする。以下、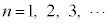 に対して、点
に対して、点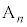 を通りy軸に平行な直線と直線kとの交点を
を通りy軸に平行な直線と直線kとの交点を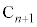 ,点
,点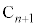 を通りx軸に平行な直線と直線
を通りx軸に平行な直線と直線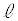 との交点を
との交点を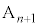 とする。
とする。
(1) 点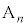 ,
,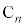 の座標を求めよ。
の座標を求めよ。 (2) △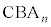 の面積
の面積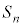 を求めよ。
を求めよ。 (3) 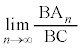 を求めよ。
を求めよ。 [解答へ]
[4] nを正の整数とし、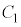 ,・・・,
,・・・,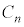 をn枚の硬貨とする。各
をn枚の硬貨とする。各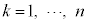 に対し、硬貨
に対し、硬貨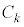 を投げて表が出る確率を
を投げて表が出る確率を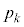 ,裏が出る確率を
,裏が出る確率を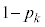 とする。このn枚の硬貨を同時に投げ、表が出た硬貨の枚数が奇数であれば成功、というゲームを考える。
とする。このn枚の硬貨を同時に投げ、表が出た硬貨の枚数が奇数であれば成功、というゲームを考える。
(1) 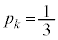 (
(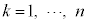 )のとき、このゲームで成功する確率
)のとき、このゲームで成功する確率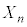 を求めよ。
を求めよ。 (2) 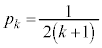 (
(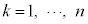 )のとき、このゲームで成功する確率
)のとき、このゲームで成功する確率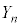 を求めよ。
を求めよ。 (3) 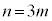 (m:正の整数)で、
(m:正の整数)で、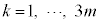 に対して
に対して とする。このゲームで成功する確率を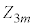 とするとき、
とするとき、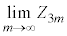 を求めよ。
を求めよ。 [解答へ]
[5] 整数の組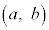 に対して2次式
に対して2次式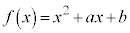 を考える。方程式
を考える。方程式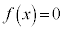 の複素数の範囲のすべての解αに対して
の複素数の範囲のすべての解αに対して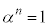 となる正の整数nが存在するような組
となる正の整数nが存在するような組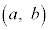 をすべて求めよ。
をすべて求めよ。
[解答へ]
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
東工大数学TOP 数学TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2024(有)りるらる 苦学楽学塾 随時入会受付中!理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。