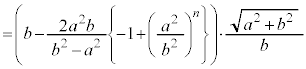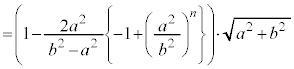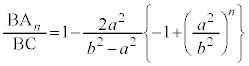���H�吔�w'24�N�O��[3]
xy���ʏ�ɁA�_A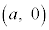 �CB
�CB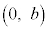 �CC
�CC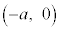 (������
(������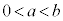 )���Ƃ�B�_A�CB��ʂ钼����
)���Ƃ�B�_A�CB��ʂ钼����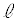 �Ƃ��A�_C��ʂ����BC�ɐ����Ȓ�����k�Ƃ���B����ɁA�_A��ʂ�y���ɕ��s�Ȓ����ƒ���k�Ƃ̌�_��
�Ƃ��A�_C��ʂ����BC�ɐ����Ȓ�����k�Ƃ���B����ɁA�_A��ʂ�y���ɕ��s�Ȓ����ƒ���k�Ƃ̌�_��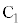 �Ƃ��A�_
�Ƃ��A�_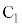 ��ʂ�x���ɕ��s�Ȓ����ƒ���
��ʂ�x���ɕ��s�Ȓ����ƒ���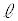 �Ƃ̌�_��
�Ƃ̌�_��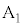 �Ƃ���B�ȉ��A
�Ƃ���B�ȉ��A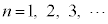 �ɑ��āA�_
�ɑ��āA�_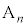 ��ʂ�y���ɕ��s�Ȓ����ƒ���k�Ƃ̌�_��
��ʂ�y���ɕ��s�Ȓ����ƒ���k�Ƃ̌�_��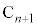 �C�_
�C�_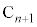 ��ʂ�x���ɕ��s�Ȓ����ƒ���
��ʂ�x���ɕ��s�Ȓ����ƒ���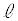 �Ƃ̌�_��
�Ƃ̌�_��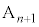 �Ƃ���B
�Ƃ���B
(1) �_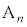 �C
�C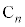 �̍��W�����߂�B
�̍��W�����߂�B (2) ��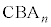 �̖ʐ�
�̖ʐ�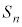 �����߂�B
�����߂�B (3) 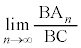 �����߂�B
�����߂�B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@�������łƂĂ��v�����Ȃ��悤�Ȕ��z������A�����ƃ��N�ɉ��邱�Ƃ��\�Ȃ悤�ł����A�ȉ��ł͑f����2���ԑQ�����̖��Ƃ��ĉ��܂��B�v�Z���җ�Ŏ��ԕs���ɂȂ肩�˂܂��A�ȒP�ȉ�@��1���ԒNj�����̂ł���A����1���ԂŌv�Z���Ă��܂��������悢�Ǝv���܂��B
�_A�CB��ʂ�����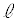 �F
�F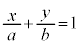 �@����@
�@����@
����BC�̌X����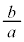 �C����������Ȓ����̌X����
�C����������Ȓ����̌X����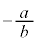 �C
�C
����k�F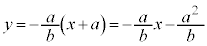 �@����A
�@����A
�_A��ʂ�y���ɕ��s�Ȓ����F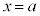 �ƒ���k�Ƃ̌�_
�ƒ���k�Ƃ̌�_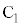 �́A�A��
�́A�A��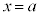 �Ƃ��āA
�Ƃ��āA
����āA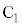 �̍��W��
�̍��W��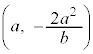 �@����B
�@����B
�_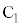 ��ʂ�x���ɕ��s�Ȓ����F
��ʂ�x���ɕ��s�Ȓ����F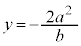 �ƒ���
�ƒ���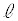 �Ƃ̌�_
�Ƃ̌�_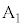 �́A�@��
�́A�@��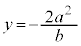 �Ƃ��āA
�Ƃ��āA
����āA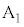 �̍��W��
�̍��W��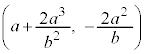 �@����C
�@����C
(1) 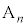 �̍��W��
�̍��W��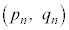 �Ƃ��܂��B�C���A
�Ƃ��܂��B�C���A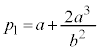 �C
�C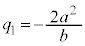 �@����D
�@����D �_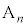 ��ʂ�y���ɕ��s�Ȓ����F
��ʂ�y���ɕ��s�Ȓ����F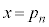 �ƒ���k�Ƃ̌�_
�ƒ���k�Ƃ̌�_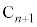 �́A�A��
�́A�A��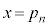 �Ƃ��āA
�Ƃ��āA ����āA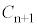 �̍��W��
�̍��W��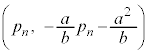 �@����E
�@����E
�_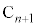 ��ʂ�x���ɕ��s�Ȓ����ƒ���
��ʂ�x���ɕ��s�Ȓ����ƒ���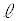 �Ƃ̌�_
�Ƃ̌�_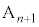 �́A�@��
�́A�@��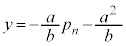 �Ƃ��āA
�Ƃ��āA ����āA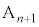 �̍��W��
�̍��W��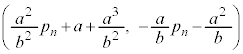
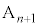 �̍��W��
�̍��W��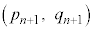 �Ȃ̂ŁA
�Ȃ̂ŁA �F�ŁA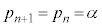 �Ƃ����ƁA
�Ƃ����ƁA �F�|�H���A
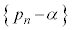 �́A����F
�́A����F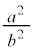 �C�����F
�C�����F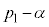 �����䐔���ł��B�D�C�I���A
�����䐔���ł��B�D�C�I���A����āA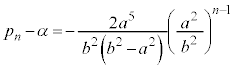 �C�I���A
�C�I���A 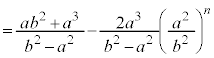
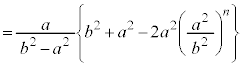 �@����J
�@����J�G�ɑ�����āA
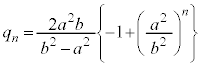 �@����K
�@����K�E���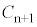 �̍��W��
�̍��W��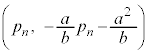 �ł����A����͇G���
�ł����A����͇G���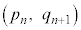 �Ȃ̂ŁA
�Ȃ̂ŁA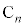 �̍��W��
�̍��W��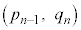 �ł��B�J�C�K���A
�ł��B�J�C�K���A
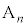 �̍��W�́A
�̍��W�́A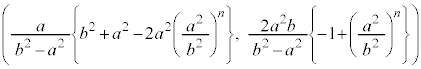 �C
�C
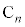 �̍��W�́A
�̍��W�́A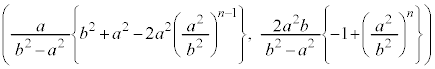 .....[��]
.....[��]
(2) ��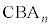 �̖ʐ�
�̖ʐ�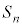 �́A��ABC�̖ʐςƁ�
�́A��ABC�̖ʐςƁ�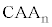 �̖ʐς̘a�Ƃ��āA
�̖ʐς̘a�Ƃ��āA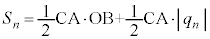 �ŗ^�����܂��B
�ŗ^�����܂��B ��ABC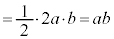
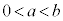 ���
���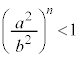 �Ȃ̂ŁA�K��p���āA
�Ȃ̂ŁA�K��p���āA��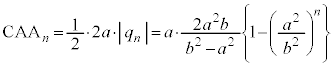
�� 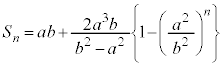 ......[��]
......[��]
(3) 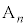 ��x���W�F(B��y���W�|
��x���W�F(B��y���W�|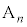 ��y���W) = OA�FOB = a�Fb ���A
��y���W) = OA�FOB = a�Fb ���A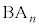 �F(B��y���W�|
�F(B��y���W�|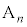 ��y���W) =
��y���W) = 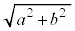 �Fb
�Fb �K��p���āA
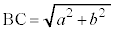 ���A
���A������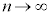 �Ƃ���ƁA
�Ƃ���ƁA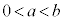 ���
���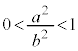 �C
�C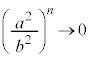 �@(���䐔��̋Ɍ����Q��)��
�@(���䐔��̋Ɍ����Q��)�� 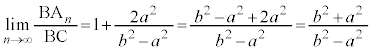 ......[��]
......[��]
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���H�吔�wTOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B 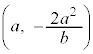 �@����B
�@����B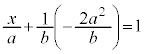
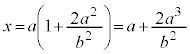
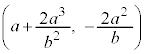 �@����C
�@����C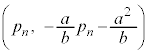 �@����E
�@����E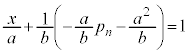
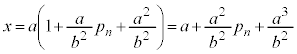
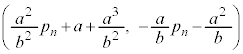
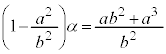
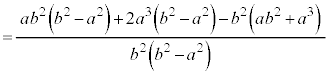
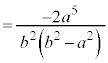
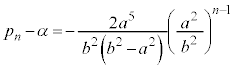 �C�I���A
�C�I���A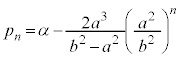
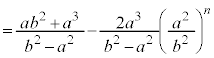
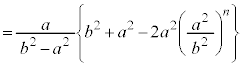 �@����J
�@����J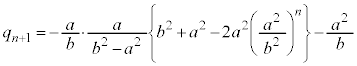
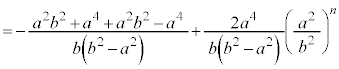
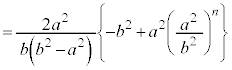
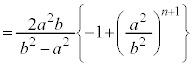
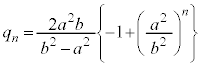 �@����K
�@����K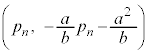 �ł����A����͇G���
�ł����A����͇G���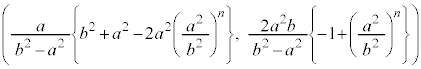 �C
�C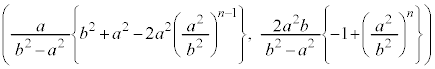 .....[��]
.....[��]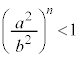 �Ȃ̂ŁA�K��p���āA
�Ȃ̂ŁA�K��p���āA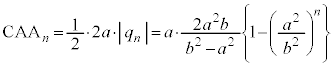
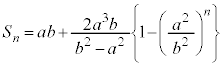 ......[��]
......[��]