���H�吔�w'24�N�O��[1]
xy���ʏ�̋Ȑ�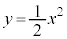 �ɁA�_
�ɁA�_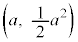 (
(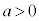 )�Őڂ���~�̂����Ay���̐��̕����ɂ��ڂ�����̂�
)�Őڂ���~�̂����Ay���̐��̕����ɂ��ڂ�����̂�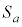 �Ƃ����Ba�����̎������Ƃ���
�Ƃ����Ba�����̎������Ƃ���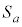 �̒��S�̋O�Ղ�C�C�Ƃ���
�̒��S�̋O�Ղ�C�C�Ƃ���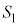 �̒��S��P�Ƃ���B
�̒��S��P�Ƃ���B
(1) �_P�̍��W�����߂�B
(2) �_P�ɂ�����Ȑ�C�̐ڐ��̌X�������߂�B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@�ܘ_�A(2)��������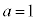 �Ƃ���(1)�̓����A�Ƃ���A�����I�Ȃ̂͊m���ł����A�ȉ��ł́A�o��҂�������(1)��u�����Ӑ}������ʼn��܂��B�r���Ń~�X�����Ă���Ȍ�̗��ꂪ�ς���Ă��܂��A(1)�����ł��ł��Ă�����i���C���ɓ͂��̂ɁA�D�G�Ȏ��ƕ������Ă��Ă��ߑ������s���i�ɂ����o��������̂ł��傤�B
�Ƃ���(1)�̓����A�Ƃ���A�����I�Ȃ̂͊m���ł����A�ȉ��ł́A�o��҂�������(1)��u�����Ӑ}������ʼn��܂��B�r���Ń~�X�����Ă���Ȍ�̗��ꂪ�ς���Ă��܂��A(1)�����ł��ł��Ă�����i���C���ɓ͂��̂ɁA�D�G�Ȏ��ƕ������Ă��Ă��ߑ������s���i�ɂ����o��������̂ł��傤�B
�~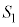 �ƋȐ�
�ƋȐ�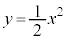 �Ƃ̐ړ_��
�Ƃ̐ړ_��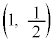 �ł��B
�ł��B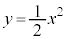 �����������ƁA
�����������ƁA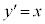 �C
�C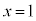 �ɂ������ڐ��̌X����1�C�@���̌X����
�ɂ������ڐ��̌X����1�C�@���̌X����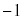 �ł��B�_
�ł��B�_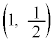 ��ʂ�@��
��ʂ�@��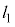 �́A
�́A
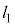 �F
�F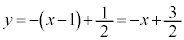 �@����@
�@����@(1) �_P�͖@��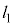 ��ɑ��݂�(�~�ƕ��������Q��)�A���̍��W��
��ɑ��݂�(�~�ƕ��������Q��)�A���̍��W��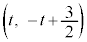 �Ƃ����ƁA�~
�Ƃ����ƁA�~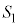 ��y���ɐڂ���̂ł��̔��a��t �ł���A�_P�Ɛړ_
��y���ɐڂ���̂ł��̔��a��t �ł���A�_P�Ɛړ_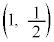 �Ƃ̋�����t �ł��B����āA
�Ƃ̋�����t �ł��B����āA �����̊e�X�ɂ��āA�_P��y���W(y���Ƃ̐ړ_��y���W�������ł�)�́A�@��p���āA
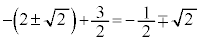 (��������)
(��������)y���̐��̕����Ɛڂ���̂ŁA�A�̂����A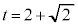 �͕s�K�ł��B
�͕s�K�ł��B
����āA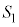 �̒��SP�́A
�̒��SP�́A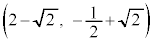 ......[��]
......[��]
(2) �~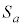 �ƋȐ�
�ƋȐ�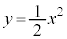 �Ƃ̐ړ_
�Ƃ̐ړ_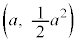 �ɂ�����ڐ��̌X����
�ɂ�����ڐ��̌X����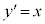 ���a�C�@���̌X����
���a�C�@���̌X����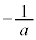 �ł��B�_
�ł��B�_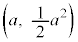 ��ʂ�@��
��ʂ�@��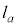 �́A
�́A 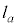 �F
�F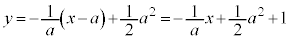 �@����B
�@����B���D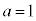 �Ƃ����
�Ƃ����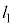 �ƈ�v���܂��B
�ƈ�v���܂��B �~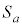 �̒��S
�̒��S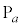 �͖@��
�͖@��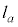 ��ɑ��݂��A���̍��W��
��ɑ��݂��A���̍��W��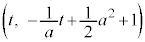 �Ƃ����ƁA�~
�Ƃ����ƁA�~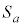 ��y���ɐڂ���̂ł��̔��a��t �ł���A�_
��y���ɐڂ���̂ł��̔��a��t �ł���A�_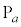 �Ɛړ_
�Ɛړ_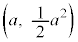 �Ƃ̋�����t �ł��B����āA
�Ƃ̋�����t �ł��B����āA �� 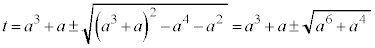 �@����C
�@����C
�����̊e�X�ɂ��āA�_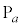 ��y���W(y���Ƃ̐ړ_��y���W�������ł�)�́A�B��p���āA
��y���W(y���Ƃ̐ړ_��y���W�������ł�)�́A�B��p���āA 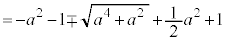
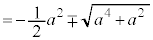 (��������)
(��������) y���̐��̕����Ɛڂ���̂ŁA�C�̂����A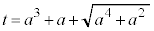 �͕s�K�ł��B
�͕s�K�ł��B
����āA�_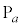 �̍��W��
�̍��W��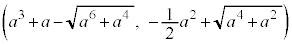 �ł��B
�ł��B ���D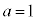 �Ƃ���ƁA
�Ƃ���ƁA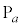 �̍��W��
�̍��W��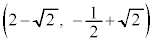 �ƂȂ�P�ƈ�v���܂��B
�ƂȂ�P�ƈ�v���܂��B �O��C��̓_��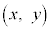 �Ƃ��āA
�Ƃ��āA 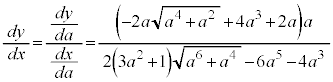 �@(��
�@(�� 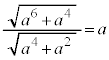 )
)������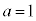 �Ƃ��āAP�ɂ�����ڐ��̌X���́A
�Ƃ��āAP�ɂ�����ڐ��̌X���́A 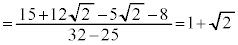 ......[��]
......[��]
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���H�吔�wTOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B 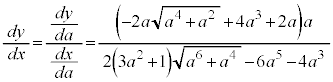 �@(��
�@(�� 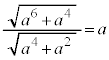 )
)