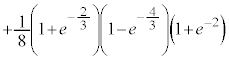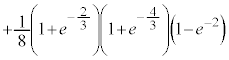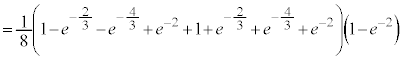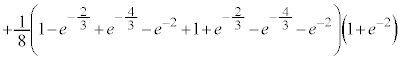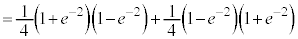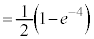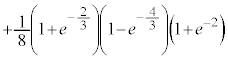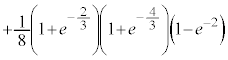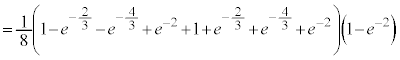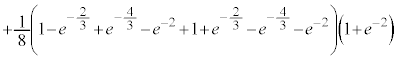���H�吔�w'24�N�O��[4]
n�𐳂̐����Ƃ��A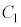 �C�E�E�E�C
�C�E�E�E�C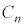 ��n���̍d�݂Ƃ���B�e
��n���̍d�݂Ƃ���B�e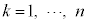 �ɑ��A�d��
�ɑ��A�d��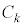 �𓊂��ĕ\���o��m����
�𓊂��ĕ\���o��m����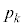 �C�����o��m����
�C�����o��m����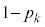 �Ƃ���B����n���̍d�݂��ɓ����A�\���o���d�݂̖�������ł���ΐ����A�Ƃ����Q�[�����l����B
�Ƃ���B����n���̍d�݂��ɓ����A�\���o���d�݂̖�������ł���ΐ����A�Ƃ����Q�[�����l����B
(1) 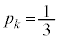 (
(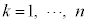 )�̂Ƃ��A���̃Q�[���Ő�������m��
)�̂Ƃ��A���̃Q�[���Ő�������m��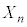 �����߂�B
�����߂�B (2) 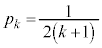 (
(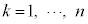 )�̂Ƃ��A���̃Q�[���Ő�������m��
)�̂Ƃ��A���̃Q�[���Ő�������m��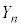 �����߂�B
�����߂�B (3) 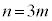 (m�F���̐���)�ŁA
(m�F���̐���)�ŁA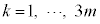 �ɑ���
�ɑ��� �Ƃ���B���̃Q�[���Ő�������m����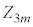 �Ƃ���Ƃ��A
�Ƃ���Ƃ��A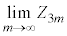 �����߂�B
�����߂�B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@�{���[3]�ɑ����āA2���ԑQ������p���ĉł��܂��B(3)�͂�₱�����v�Z���������܂��B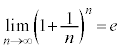 �͌����ł����A
�͌����ł����A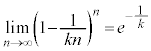 �͌����Ƃ͌����Ȃ��̂ŁA�������œ�����悤�ɂ��Ă����܂��傤�B
�͌����Ƃ͌����Ȃ��̂ŁA�������œ�����悤�ɂ��Ă����܂��傤�B
(1) 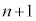 ���̍d�ݓ����Ő�������̂́An���̍d�ݓ����Ő���(�m��
���̍d�ݓ����Ő�������̂́An���̍d�ݓ����Ő���(�m��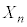 )���āA
)���āA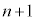 ���ڂŗ����o��(�m��
���ڂŗ����o��(�m��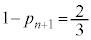 )���An���̍d�ݓ����Ő�������(�m��
)���An���̍d�ݓ����Ő�������(�m��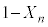 )�A
)�A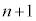 ���ڂɕ\���o��(�m��
���ڂɕ\���o��(�m��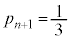 )�ꍇ�ł��B����āA
)�ꍇ�ł��B����āA �@�|�A���A
����āA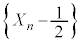 �́A����F
�́A����F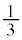 �C�����F
�C�����F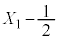 �����䐔���ł��B�d��1���̂Ƃ���������m���́A1�������ĕ\���o��m����
�����䐔���ł��B�d��1���̂Ƃ���������m���́A1�������ĕ\���o��m����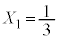 �C
�C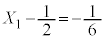 �ł��B����āA
�ł��B����āA �� 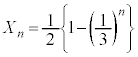 ......[��]
......[��]
(2) 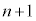 ���̍d�ݓ����Ő�������̂́An���̍d�ݓ����Ő���(�m��
���̍d�ݓ����Ő�������̂́An���̍d�ݓ����Ő���(�m��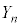 )���āA
)���āA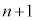 ���ڂŗ����o��(�m��
���ڂŗ����o��(�m��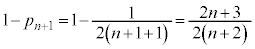 )���An���̍d�ݓ����Ő�������(�m��
)���An���̍d�ݓ����Ő�������(�m��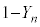 )�A
)�A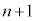 ���ڂɕ\���o��(�m��
���ڂɕ\���o��(�m��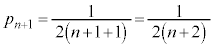 )�ꍇ�ł��B����āA
)�ꍇ�ł��B����āA 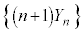 �͌����F
�͌����F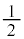 �C�����F
�C�����F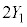 �����������ł��B�d��1���̂Ƃ���������m���́A1�������ĕ\���o��m����
�����������ł��B�d��1���̂Ƃ���������m���́A1�������ĕ\���o��m����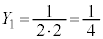 �C
�C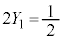 �ł��B����āA
�ł��B����āA�� 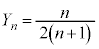 .....[��]
.....[��]
(3) 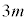 ���̍d�݂�m�������čl���܂��Bm���̍d�݂̊e��𓊂��āA�\���o��m����p�Ƃ��܂��B
���̍d�݂�m�������čl���܂��Bm���̍d�݂̊e��𓊂��āA�\���o��m����p�Ƃ��܂��B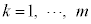 ��m���̍d�݂ɂ��Ă�
��m���̍d�݂ɂ��Ă�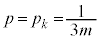 �C
�C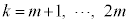 ��m���̍d�݂ɂ��Ă�
��m���̍d�݂ɂ��Ă�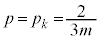 �C
�C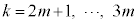 ��m���̍d�݂ɂ��Ă�
��m���̍d�݂ɂ��Ă�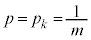 �ł��B
�ł��B m���̍d�ݓ����Ő�������m����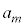 �Ƃ��܂��B
�Ƃ��܂��B
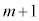 ���̍d�ݓ����Ő�������̂́Am���̍d�ݓ����Ő���(�m��
���̍d�ݓ����Ő�������̂́Am���̍d�ݓ����Ő���(�m��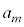 )���āA
)���āA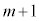 ���ڂŗ����o��(�m��
���ڂŗ����o��(�m��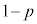 )���Am���̍d�ݓ����Ő�������(�m��
)���Am���̍d�ݓ����Ő�������(�m��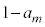 )�A
)�A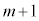 ���ڂɕ\���o��(�m��p)�ꍇ�ł��B����āA
���ڂɕ\���o��(�m��p)�ꍇ�ł��B����āA �B�|�C���A
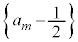 �́A����F
�́A����F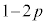 �C�����F
�C�����F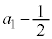 �̓��䐔��ł��B�d��1���̂Ƃ���������m���́A1�������ĕ\���o��m����
�̓��䐔��ł��B�d��1���̂Ƃ���������m���́A1�������ĕ\���o��m����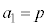 �C
�C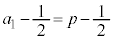 �ł��B����āA
�ł��B����āA�D�ɂ�����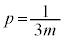 �̂Ƃ��A
�̂Ƃ��A 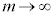 �Ƃ���ƇE(
�Ƃ���ƇE(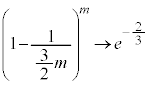 �ƍl����)��p���āA
�ƍl����)��p���āA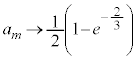 ���A
���A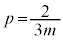 �@����F
�@����F���l�ɁA�D�ɂ�����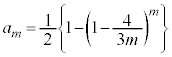 �̂Ƃ��A
�̂Ƃ��A 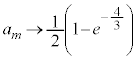 �Ƃ���ƇE(
�Ƃ���ƇE(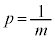 �ƍl����)��p���āA
�ƍl����)��p���āA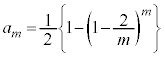 �@����G
�@����G���l�ɁA�D�ɂ�����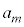 �̂Ƃ��A
�̂Ƃ��A 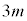 �Ƃ���ƇE(
�Ƃ���ƇE(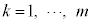 �ƍl����)��p���āA
�ƍl����)��p���āA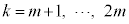 �@����H
�@����H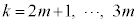 ���̍d�݂𓊂��Đ�������̂́A
���̍d�݂𓊂��Đ�������̂́A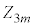 �ɑ���m���̍d�ݓ����ŕ\���o�������A
�ɑ���m���̍d�ݓ����ŕ\���o�������A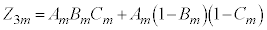 �ɑ���m���̍d�ݓ����ŕ\���o�������A
�ɑ���m���̍d�ݓ����ŕ\���o�������A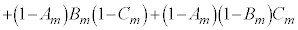 �ɑ���m���̍d�ݓ����ŕ\���o�������A�ɂ��āA
�ɑ���m���̍d�ݓ����ŕ\���o�������A�ɂ��āA
��A��A��A�ƂȂ邩�A��A�����A�����A�ƂȂ邩�A�����A��A�����A�ƂȂ邩�A�����A�����A��A�ƂȂ�ꍇ�ł��B���̊m��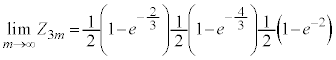 �́A
�́A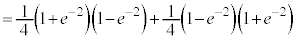
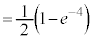 ......[��]
......[��]
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���H�吔�wTOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B 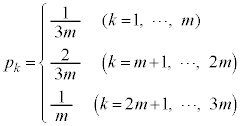
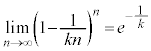 �͌����Ƃ͌����Ȃ��̂ŁA�������œ�����悤�ɂ��Ă����܂��傤�B
�͌����Ƃ͌����Ȃ��̂ŁA�������œ�����悤�ɂ��Ă����܂��傤�B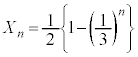 ......[��]
......[��]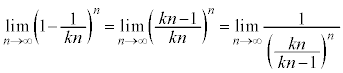
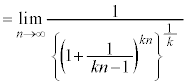
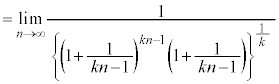
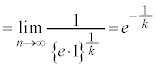 �@����E
�@����E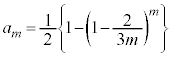 �@(���̂Ƃ���
�@(���̂Ƃ���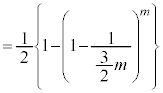
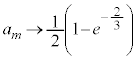 ���A
���A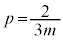 �@����F
�@����F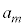 �@(���̂Ƃ���
�@(���̂Ƃ���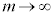
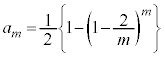 �@����G
�@����G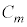 �@(���̂Ƃ���
�@(���̂Ƃ���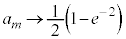
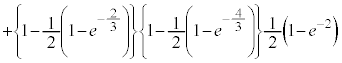 �C
�C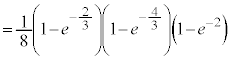 �C
�C