���H�吔�w'24�N�O��[5]
�����̑g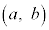 �ɑ���2����
�ɑ���2����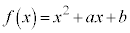 ���l����B������
���l����B������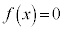 �̕��f���͈̔͂̂��ׂẲ�α�ɑ���
�̕��f���͈̔͂̂��ׂẲ�α�ɑ���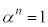 �ƂȂ鐳�̐���n�����݂���悤�ȑg
�ƂȂ鐳�̐���n�����݂���悤�ȑg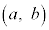 �����ׂċ��߂�B
�����ׂċ��߂�B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@�ȉ��ł́A���}��2���������̖��Ƃ��ĉ��܂��B�����̐������Ɠ��l�A�K�v�����Œ��ׂ鐮���͈̔͂��i��A��ӂ������ǂ����A�V���~�Ԃ��Œ��ׂ邱�Ƃɂ��A�H�v���Ȃ��Ă��[���Ɏ��ԓ��ɉł��܂��B
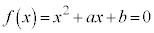 �@����@
�@����@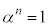 ���
���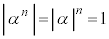 �C�����A
�C�����A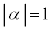 �C����āA
�C����āA
(n�͐������Ȃ̂ŁA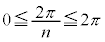 )�Ƃ����܂��B
)�Ƃ����܂��B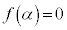 ���A
���A
�h�E���A�u���̒藝���A
�����(���f���̌v�Z���Q��)�A
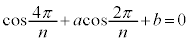 �@����B
�@����B
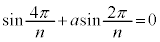 �@����C
�@����C
����āA
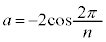 �@����D
�@����D
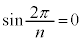 �@����E
�@����E
�E����������n��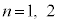 �Ɍ����܂��B
�Ɍ����܂��B
�E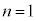 �̂Ƃ��A�A���A
�̂Ƃ��A�A���A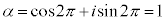
�@���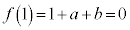
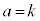 (k�F����)�Ƃ����ƁA
(k�F����)�Ƃ����ƁA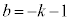
���̂Ƃ��A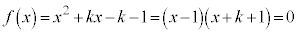
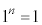 �ł����A
�ł����A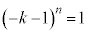 �ƂȂ�̂́A
�ƂȂ�̂́A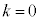 ��n�������̂Ƃ��ł��B
��n�������̂Ƃ��ł��B
����āA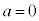 �C
�C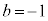
�E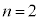 �̂Ƃ��A�A���A
�̂Ƃ��A�A���A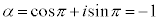
�@���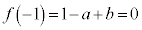
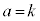 (k�F����)�Ƃ����ƁA
(k�F����)�Ƃ����ƁA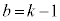
���̂Ƃ��A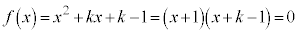
n�������ł����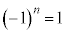 �ƂȂ�܂����A
�ƂȂ�܂����A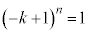 �ƂȂ�̂́A
�ƂȂ�̂́A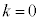 �̂Ƃ������ł��B
�̂Ƃ������ł��B
����āA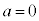 �C
�C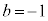
�D�̂Ƃ��A�B���A
�� 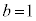
�܂��D���A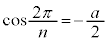
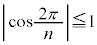 ���
���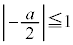 �C�����A
�C�����A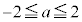
�����������a�́A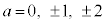
�E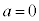 �C
�C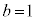 �̂Ƃ��A
�̂Ƃ��A 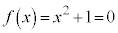 �C
�C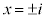 n��4�̔{���̂Ƃ�
n��4�̔{���̂Ƃ�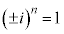 �ƂȂ�̂ŁA���̏ꍇ�͓K�ł��B
�ƂȂ�̂ŁA���̏ꍇ�͓K�ł��B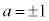 �C
�C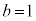 �̂Ƃ��A
�̂Ƃ��A
���̉�α�ɂ��ẮA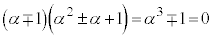 (��������)����āA
(��������)����āA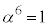 �ƂȂ�̂ŁA���̏ꍇ�͓K�ł��B
�ƂȂ�̂ŁA���̏ꍇ�͓K�ł��B �E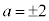 �C
�C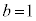 �̂Ƃ��A
�̂Ƃ��A 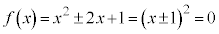 �C
�C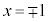
�ǂ���ɂ��Ă�2�悷���1�ɂȂ�̂ŁA���̏ꍇ�͓K�ł��B
�ȏ���A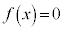 �̂��ׂẲ�α�ɑ���
�̂��ׂẲ�α�ɑ���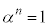 �ƂȂ鐳�̐���n�����݂���悤�ȑg
�ƂȂ鐳�̐���n�����݂���悤�ȑg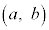 �́A
�́A
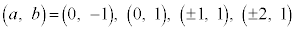 ......[��]
......[��]
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���H�吔�wTOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B