���H�吔�w'24�N�O��[2]
�����S�̂��`��ɂ������\�Ȋ�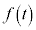 �C
�C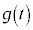 ������6�̏��������Ă���Ƃ���B
������6�̏��������Ă���Ƃ���B
���̂Ƃ��A
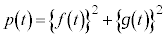 �C
�C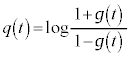
(1) 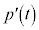 �����߂�B
�����߂�B (2) 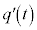 �͒萔���ł��邱�Ƃ������B
�͒萔���ł��邱�Ƃ������B (3) 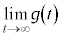 �����߂�B
�����߂�B (4) 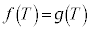 �ƂȂ鐳�̎���T�ɑ��āA�}��ϐ��\�����ꂽ���ʋȐ�
�ƂȂ鐳�̎���T�ɑ��āA�}��ϐ��\�����ꂽ���ʋȐ�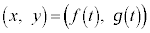 (
(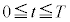 )�̒��������߂�B
)�̒��������߂�B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@���H��Ƃ��Ă͖ڐV�����e�[�}�̖��ł����A���Ղȓ��e�ŁA���̖��͗��Ƃ��܂���B
��蕶���A
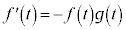 �@����@
�@����@
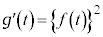 �@����A
�@����A
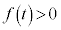 �@����B
�@����B
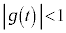 �@����C
�@����C
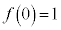 �@����D
�@����D
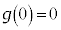 �@����E
�@����E
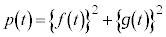 �@����F
�@����F
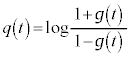 �@����G
�@����G
(1) �F�����������ƁA�@�C�A��p���āA
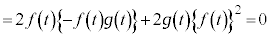 ......[��]
......[��]�]����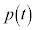 �͒萔���ŁA�F��
�͒萔���ŁA�F��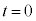 �Ƃ���ƁA�D�C�E���A
�Ƃ���ƁA�D�C�E���A �܂�A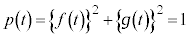 �@����H
�@����H
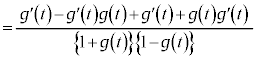
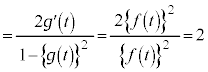 �@(�� �A�C�H)
�@(�� �A�C�H)����āA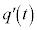 �͒萔���ł��B
�͒萔���ł��B
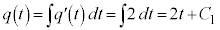 �@(
�@(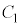 �F�萔)
�F�萔)�G��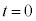 �Ƃ���ƁA�E���A
�Ƃ���ƁA�E���A 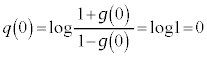 �@��
�@�� 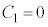 �C
�C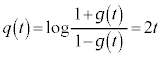
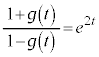 �@(�ΐ������Q��)
�@(�ΐ������Q��)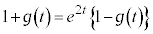 �@��
�@�� 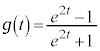 �@����I
�@����I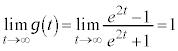 ......[��]�@����J
......[��]�@����J�܂��A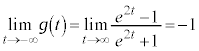 �@����K
�@����K
�A���A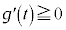 �ł���A
�ł���A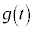 ���P���������ł��B�J�C�K���A
���P���������ł��B�J�C�K���A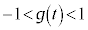 �ł���A�I�œ���ꂽ
�ł���A�I�œ���ꂽ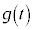 �́A�C�����܂��B
�́A�C�����܂��B
(4) �}��ϐ��\�����ꂽ���ʋȐ�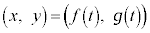 �́A�H���
�́A�H���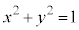 �����A���_�𒆐S�Ƃ��锼�a1�� �~ �ł��B
�����A���_�𒆐S�Ƃ��锼�a1�� �~ �ł��B 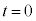 �̂Ƃ��A�D�C�E���A
�̂Ƃ��A�D�C�E���A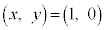 �ł��B���̓_��P�Ƃ��܂��B
�ł��B���̓_��P�Ƃ��܂��B
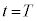 �̂Ƃ��A
�̂Ƃ��A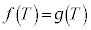 ���A
���A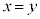 �ł��B���̂Ƃ��B���A
�ł��B���̂Ƃ��B���A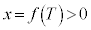
�~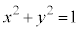 ��̓_��
��̓_��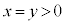 �����_��
�����_��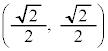 �ł���A���̓_��Q�Ƃ��܂��B�I�œ���ꂽ
�ł���A���̓_��Q�Ƃ��܂��B�I�œ���ꂽ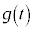 �́A
�́A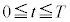 �͈̔͂ɂ����ĘA���Ȋ��ŁA���߂�Ȑ��̒����́A�~��
�͈̔͂ɂ����ĘA���Ȋ��ŁA���߂�Ȑ��̒����́A�~��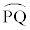 �̒����ł���A���a1�C
�̒����ł���A���a1�C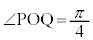 ���A
���A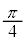 ......[��]
......[��]
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���H�吔�wTOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B 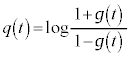
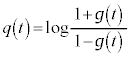 �@����G
�@����G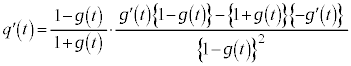
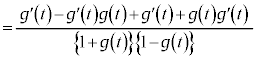
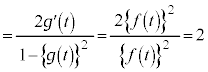 �@(�� �A�C�H)
�@(�� �A�C�H)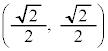 �ł���A���̓_��Q�Ƃ��܂��B�I�œ���ꂽ
�ł���A���̓_��Q�Ƃ��܂��B�I�œ���ꂽ