ÈwåHwnw'25NOú[4]
ñ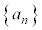 ð
ð
ÉæèèßAñ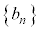 ð
ð
ÉæèèßéB½¾µA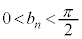 Å éàÌÆ·éB
Å éàÌÆ·éB
(1) 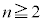 ÉεÄA
ÉεÄA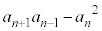 ðßæB
ðßæB (2) 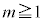 (mÍ®)ÉεÄA
(mÍ®)ÉεÄA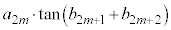 ðßæB
ðßæB (3) ³À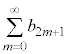 ðßæB
ðßæB
yLz±±©çLÅ·B²ÌF³Ü̲x²ððè½Aæ뵨袢½µÜ·B
yLzLͱ±ÜÅÅ·B
ð@tB{ib`ÌñÌâèÅ·ªAQ»®
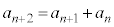 @(
@(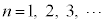 )@¥¥¥@
)@¥¥¥@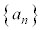 ÌÅÌûÌðÆA1C1C2C3C5C8C13C21C34C55C89C¥¥¥@ÆÈÁĢܷB
ÌÅÌûÌðÆA1C1C2C3C5C8C13C21C34C55C89C¥¥¥@ÆÈÁĢܷB
(1) 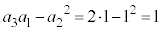 C
C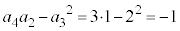 @¥¥¥A
@¥¥¥A 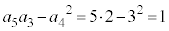 C
C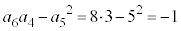
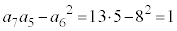 C
C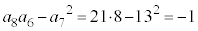
ÆÈÁÄ¢éÌÅAnªôÌÆ«É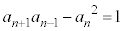 CnªïÌÆ«É
CnªïÌÆ«É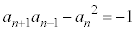 @()ÆÈÁÄ¢é±Æª\z³êéÌÅA±êðwIA[@ÉæèؾµÜ·B
@()ÆÈÁÄ¢é±Æª\z³êéÌÅA±êðwIA[@ÉæèؾµÜ·BE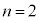 C
C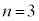 ÌÆ«A()ÍAæè¬è§¿Ü·B
ÌÆ«A()ÍAæè¬è§¿Ü·B Ekð©RƵÄA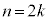 C
C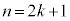 ÌÆ«()ª¬§·éƼèµÜ·BÂÜèA
ÌÆ«()ª¬§·éƼèµÜ·BÂÜèA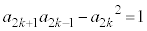 C
C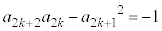 ª¬è§ÂƼèµÜ·B
ª¬è§ÂƼèµÜ·B Q»®@ðp¢éÆA
æÁÄA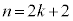 C
C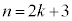 ÌÆ«à()ª¬§µÜ·B
ÌÆ«à()ª¬§µÜ·B ÈãæèAwIA[@Éæè()ª¬§µÜ·BnªôÌÆ«É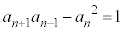 CnªïÌÆ«É
CnªïÌÆ«É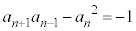 ......[]
......[] ÊðD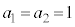 Æ@ð½·ñÌêÊ
Æ@ð½·ñÌêÊ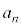 ÍAÁ«ûö®F
ÍAÁ«ûö®F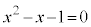 Ìð
Ìð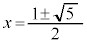 (
(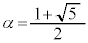 C
C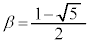 Ƶܷ)ðp¢ÄA
Ƶܷ)ðp¢ÄA Æ\¹Ü·B±êðp¢Äßé±ÆàÅ«Ü·B
(2) 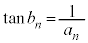 @¥¥¥C
@¥¥¥C ðp¢ÄA
(1)ÌÊÅ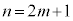 (ï)Æ·éÆA
(ï)Æ·éÆA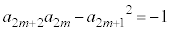 D
D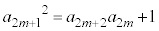 ÆÈéÌÅA
ÆÈéÌÅA 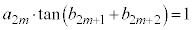 ......[]
......[]
(3) mð©RƵÄA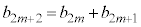 æèA
æèA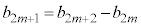 ÆÈéÌÅA
ÆÈéÌÅA 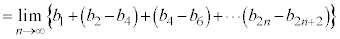
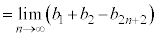 @¥¥¥D
@¥¥¥D±±ÅA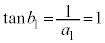 C
C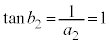 æèA
æèA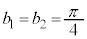 Å·B
Å·B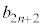 ªâèÉÈèÜ·ªA
ªâèÉÈèÜ·ªA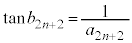 æèAñ
æèAñ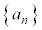 ÌÅÌûð²×éÆA
ÌÅÌûð²×éÆA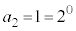 C
C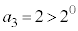 C
C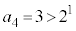 C
C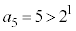 C
C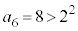 C
C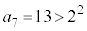 C
C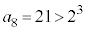 C
C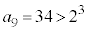 ÆÈÁÄ¢ÄA
ÆÈÁÄ¢ÄA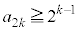 C
C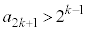 ÆÈé±Æª\ªÅ«Ü·B
ÆÈé±Æª\ªÅ«Ü·B
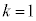 ÌÆ«A\ªÍ¬§µÜ·B
ÌÆ«A\ªÍ¬§µÜ·B
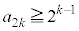 C
C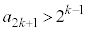 ª¬§·éÆ«A
ª¬§·éÆ«A ÆÈéÌÅAA[IÉ\ªÍ¬§µÜ·B
±êæèA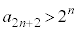 Å ÁÄA
Å ÁÄA 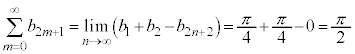 ......[]
......[]
yLz±±©çLÅ·B²ÌF³Ü̲x²ððè½Aæ뵨袢½µÜ·B
yLzLͱ±ÜÅÅ·B
@@ÈwåwTOP@@wTOP@@TOPy[WÉßé
yLz±±©çLÅ·B²ÌF³Ü̲x²ððè½Aæ뵨袢½µÜ·B
yLzLͱ±ÜÅÅ·B
eâèÌì Í
oèåwÉ®µÜ·BȨAðÍA
êwywm§ìÅ·B©2005-2025(L)èéçé êwywm üïótInåwó±lbgmêwywm(²Äàͱ¿ç)²üïÍA
ܸA±¿çÜÅ[ð
¨è¾³¢B 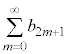 ðßæB
ðßæB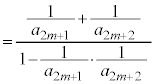
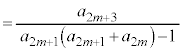
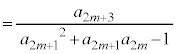
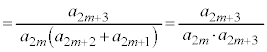 @(æ @)
@(æ @)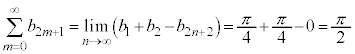 ......[]
......[]