ÈwåHwnw'25NOú[5]
(1) Ö
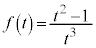 @(
@(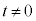 )
)̸ð²×AOtÌT`ð©¯B
(2) ÀxCyCzªAð
ð½µÈªç®Æ«Axªæè¾élÌÍÍðßæB
yLz±±©çLÅ·B²ÌF³Ü̲x²ððè½Aæ뵨袢½µÜ·B
yLzLͱ±ÜÅÅ·B
ð@÷ª@ðpµÄûö®Ìððl¦éâèÅ·B
(2) âè¶Ìð®Ìæ3®Ææ4®ÉæèA
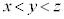 C
C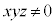 æèAxCyCzÍA0ÈOÌÙÈé3ÀÈÌÅAkðKÈÀƵÄAxCyCzÍAûö®
æèAxCyCzÍA0ÈOÌÙÈé3ÀÈÌÅAkðKÈÀƵÄAxCyCzÍAûö®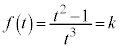 Ì0ÅÈ¢ÙÈé3ÀðÅ·(÷ª@Ìûö®ÖÌp(2)ðQÆ)B
Ì0ÅÈ¢ÙÈé3ÀðÅ·(÷ª@Ìûö®ÖÌp(2)ðQÆ)B
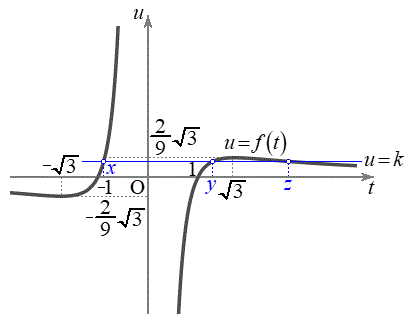 E}ɨ¢ÄA
E}ɨ¢ÄA ÌOtƼü
ÌOtƼü Ìð_ðl¦éÆA¼Òªy²(
Ìð_ðl¦éÆA¼Òªy²(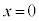 )ãÈOÉÙÈé3ð_ðÂÌÍA
)ãÈOÉÙÈé3ð_ðÂÌÍA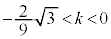 C
C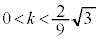 ÌêÅAxÍAûö®
ÌêÅAxÍAûö®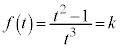 Ìð̤¿Å¬ÌàÌÅ·B
Ìð̤¿Å¬ÌàÌÅ·B
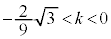 ÌÆ«AE}æè
ÌÆ«AE}æè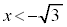 Å·B
Å·B
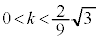 ÌÆ«AE}æèAxÍ
ÌÆ«AE}æèAxÍ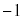 æèå«A
æèå«A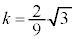 ÌÆ«Ìûö®Ìð̤¿ÌŬÌàÌ(αƵܷ)æèଳÈèÜ·B
ÌÆ«Ìûö®Ìð̤¿ÌŬÌàÌ(αƵܷ)æèଳÈèÜ·B
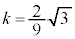 ÌÆ«
ÌÆ«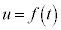 ÌOtƼü
ÌOtƼü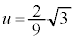 Í
Í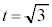 ɨ¢ÄÚ·éÌűÌÆ«Ìûö®A
ɨ¢ÄÚ·éÌűÌÆ«Ìûö®A 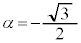 @(ÂÜèA
@(ÂÜèA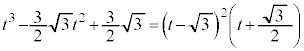 )ÈãæèAxªæè¾éÍÍÍA
)ÈãæèAxªæè¾éÍÍÍA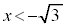 C
C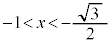 .......[]
.......[]
yLz±±©çLÅ·B²ÌF³Ü̲x²ððè½Aæ뵨袢½µÜ·B
yLzLͱ±ÜÅÅ·B
@@ÈwåwTOP@@wTOP@@TOPy[WÉßé
yLz±±©çLÅ·B²ÌF³Ü̲x²ððè½Aæ뵨袢½µÜ·B
yLzLͱ±ÜÅÅ·B
eâèÌì Í
oèåwÉ®µÜ·BȨAðÍA
êwywm§ìÅ·B©2005-2025(L)èéçé êwywm üïótInåwó±lbgmêwywm(²Äàͱ¿ç)²üïÍA
ܸA±¿çÜÅ[ð
¨è¾³¢B 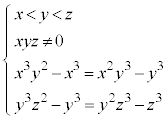
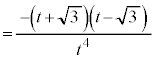
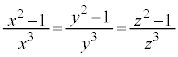
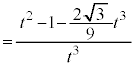
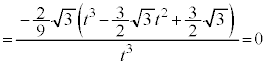
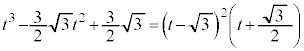 )
)