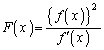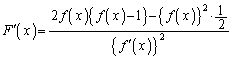���H�吔�w'96�N�O��[4]
��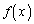 �͔����\�Ŏ���(�C)�C(��)�C(�n)���݂������̂Ƃ���B
�͔����\�Ŏ���(�C)�C(��)�C(�n)���݂������̂Ƃ���B
(�C)�@ �̂Ƃ�
�̂Ƃ�
(��)�@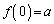 �@(�������A
�@(�������A )
) (�n)�@�Ȑ�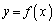 ��̓_P
��̓_P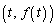 (
(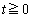 )�ɂ�����ڐ���x���Ƃ̌�_��Q�C�@����x���Ƃ̌�_��R�Ƃ����Ƃ��A����QR�̒���
)�ɂ�����ڐ���x���Ƃ̌�_��Q�C�@����x���Ƃ̌�_��R�Ƃ����Ƃ��A����QR�̒���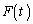 �͊W��
�͊W�� ���݂����B
���̂Ƃ����̖₢�ɓ�����B
(1)  ��
��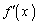 �͒P�������ŁA
�͒P�������ŁA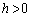 �ɑ�
�ɑ� ���݂������Ƃ������B
���݂������Ƃ������B (2) �_P���Ȑ�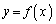 (
(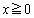 )����Ƃ�
)����Ƃ�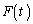 �̍ŏ��l�����߂�B
�̍ŏ��l�����߂�B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@�ŋ߁A���܂茩�����Ȃ��Ȃ��� �̂܂܍l���Ă䂯����ł��B�����������ۓI�ȕ��͋C��ь���������������̂ł����A��̓I��
�̂܂܍l���Ă䂯����ł��B�����������ۓI�ȕ��͋C��ь���������������̂ł����A��̓I�� �̌`���^�����Ă�������A�ʓ|�Ȍv�Z�����Ȃ��Ă��ޕ��������N�Ȗ��Ǝv���Ē����������̂ł��B
�̌`���^�����Ă�������A�ʓ|�Ȍv�Z�����Ȃ��Ă��ޕ��������N�Ȗ��Ǝv���Ē����������̂ł��B
(1) �_P �ɂ������ڐ��́A
�ɂ������ڐ��́A x���Ƃ̌�_Q��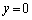 �Ƃ��āA
�Ƃ��āA 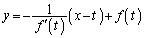 �@(
�@(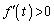 )
)x���Ƃ̌�_R��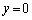 �Ƃ��āA
�Ƃ��āA 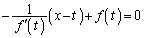
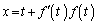 �@����A
�@����A����(�C)���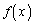 ��
��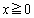 �ɂ������P�������ŁA����(��)���
�ɂ������P�������ŁA����(��)���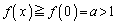
����āA�@��Q��x���W�ɂ��āA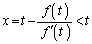
�A��R��x���W�ɂ��āA
�]���Đ���QR�̒��� �́A
�́A ����(�n)���A
����āA
t��x (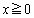 )�ɏ��������āA
)�ɏ��������āA  �@����B
�@����B���ӂ�x�Ŕ�������ƁA
 ���A
���A �@����C
�@����C
������A ��
��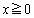 �ɂ������P�������ł��B����D
�ɂ������P�������ł��B����D
�B���A
�� 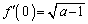
���D�����ŁA�C���A �C
�C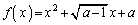 �ƂȂ�A
�ƂȂ�A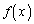 �̋�̓I�Ȍ`�����܂��Ă��܂��܂��B
�̋�̓I�Ȍ`�����܂��Ă��܂��܂��B 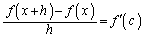 �C
�C
��������c�����݂��܂��B�D���A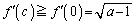
�� 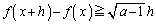
(2) ����(�n)���A �ɂ����āA
�ɂ����āA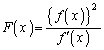
�B�C�C��p����ƁA
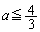 �@����E
�@����E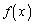 ��
��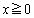 �ɂ����ĒP��������
�ɂ����ĒP��������
�ł����A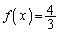 �ƂȂ�x��
�ƂȂ�x��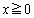 �͈̔͂ɑ��݂��邩�ǂ����͂킩��܂���B
�͈̔͂ɑ��݂��邩�ǂ����͂킩��܂���B�E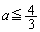 �ł���A
�ł���A ���A
���A �ƂȂ�x��
�ƂȂ�x��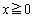 �͈̔͂ɑ��݂���̂ŁA����x��α�Ƃ��܂��B
�͈̔͂ɑ��݂���̂ŁA����x��α�Ƃ��܂��B �͒P�������Ȃ̂ŁA
�͒P�������Ȃ̂ŁA �ɂ����Ă�
�ɂ����Ă�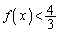 �C
�C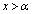 �ɂ����Ă�
�ɂ����Ă�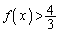
�܂��A�B���A
�� 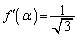 (
(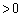 )����āA
)����āA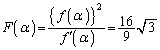 �����\���A
�����\���A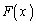 ��
��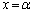 �ɂ����čŏ��l
�ɂ����čŏ��l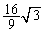 ���Ƃ�܂�(���̑������Q��)�B
���Ƃ�܂�(���̑������Q��)�B �E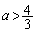 �̂Ƃ��ɂ́A
�̂Ƃ��ɂ́A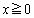 �ɂ�����
�ɂ�����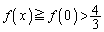 �ƂȂ�̂ŁA
�ƂȂ�̂ŁA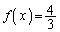 �ƂȂ�x�͑��݂��܂���B�E�ɂ����āA
�ƂȂ�x�͑��݂��܂���B�E�ɂ����āA ���
���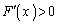 �ƂȂ�A
�ƂȂ�A ��
�� �ɂ����ĒP�������B
�ɂ����ĒP�������B �� 
�ȏ���A �̍ŏ��l�́A
�̍ŏ��l�́A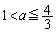 �̂Ƃ�
�̂Ƃ�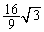 �C
�C �̂Ƃ�
�̂Ƃ� ......[��]
......[��]
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���H�吔�wTOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B