���嗝�n���w'05�N�O��[1]
 �ɑ�
�ɑ�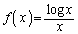 �Ƃ���B
�Ƃ���B
(1) 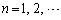 �ɑ�
�ɑ�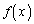 �̑�n�������́A����
�̑�n�������́A����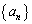 �C
�C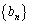 ��p����
��p���� 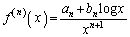 �ƕ\����邱�Ƃ������A
�ƕ\����邱�Ƃ������A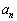 �C
�C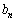 �Ɋւ���Q���������߂�B
�Ɋւ���Q���������߂�B(2) 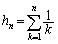 �Ƃ����B
�Ƃ����B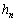 ��p����
��p����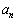 �C
�C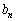 �̈�ʍ������߂�B
�̈�ʍ������߂�B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@�܂��́A(1)�ł����A����͒P�ɔ������Ă݂邾���ł��B���̔����@�̌v�Z���K�ɂ��傤�Ǘǂ��ł��B�����̊F����́A3���̓����܂Ōv�Z���Ă݂Ă��������B
���̂悤�ɂȂ�ł��傤�B
����ŁA�����̂͂��߂�3�����ǂ��Ȃ��Ă��邩�킩��܂��B
�^���ǂ���A����Ŗ��̃A�E�g���C�����ǂ߂Ă��܂����Ƃ�����܂��B
�ׂ������Ƃ�(2)�ōl���邱�Ƃɂ��āA
�Ə����邱�� ����@ �������Ă݂܂��B
(i) 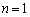 �̂Ƃ��A
�̂Ƃ��A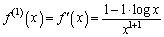 ���A
���A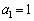 �C
�C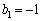 �Ƃ��āA�@�͐��藧���܂��B
�Ƃ��āA�@�͐��藧���܂��B (ii) 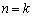 �̂Ƃ����藧�Ƃ���ƁA
�̂Ƃ����藧�Ƃ���ƁA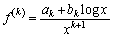 �Ə����܂��B
�Ə����܂��B ������������ƁA
�����ŁA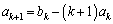 �C
�C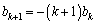 ����A �Ƃ���A
����A �Ƃ���A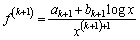 �Ə����܂��B
�Ə����܂��B
����āA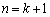 �̂Ƃ����A�@�͐��藧���܂��B
�̂Ƃ����A�@�͐��藧���܂��B (i)�C(ii)���A�S�Ă̎��R��n�ɑ��āA�@�����藧���܂��B
�悭�A"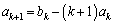 �C
�C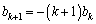 ����A �Ƃ����"�Ƃ����̂��A�Ȃ��A����ȕ��ɂ�����̂��ؖ����Ȃ��Ă悢�̂��A�ƁA�^��Ɏv���l������̂ł����A����́A
����A �Ƃ����"�Ƃ����̂��A�Ȃ��A����ȕ��ɂ�����̂��ؖ����Ȃ��Ă悢�̂��A�ƁA�^��Ɏv���l������̂ł����A����́A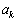 ��
��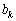 �̒l���킩���Ă���Ƃ��ɁA�A���ɂ���āA
�̒l���킩���Ă���Ƃ��ɁA�A���ɂ���āA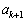 ��
��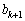 �̒l�����߂Ă��������A����ŁA
�̒l�����߂Ă��������A����ŁA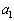 �C
�C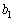 ����o�����Đ���̊e���̒l��S�ċ��߂邱�Ƃ��ł��܂��A�Ƃ����Ӗ��ł��B
����o�����Đ���̊e���̒l��S�ċ��߂邱�Ƃ��ł��܂��A�Ƃ����Ӗ��ł��B
���藧�����藧���Ȃ����A�킩��Ȃ����Ƃ���Ƃ��ćA���o�Ă����̂ł͂Ȃ��A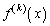 ���������
���������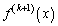 �����߂Ă݂��Ƃ���A�m���߂��Ă��ďؖ�����K�v�̂Ȃ����Ƃ���Ƃ��āA�A���o�Ă��Ă���̂ł��B
�����߂Ă݂��Ƃ���A�m���߂��Ă��ďؖ�����K�v�̂Ȃ����Ƃ���Ƃ��āA�A���o�Ă��Ă���̂ł��B
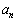 �C
�C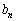 �Ɋւ����Q�����́A�A��k��n�ɏ��������āA
�Ɋւ����Q�����́A�A��k��n�ɏ��������āA 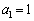 �C
�C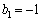
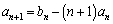 ����B�C
����B�C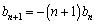 ����C ......[��]
����C ......[��]
(2) 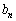 �ɂ��ẮA�C�����Ă���A
�ɂ��ẮA�C�����Ă���A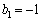 �C
�C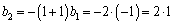 �C
�C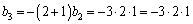 �C������ �Ƃ���Ă����A��Ԃ߂ŕ��A�����Ԃ߂Ő��Ȃ̂ŁA
�C������ �Ƃ���Ă����A��Ԃ߂ŕ��A�����Ԃ߂Ő��Ȃ̂ŁA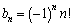 �Ƃ킩��܂��B
�Ƃ킩��܂��B ������B�ɑ������ƁA
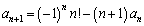 ����D
����D���̑Q�����́A���ȏ���Q�l���ł͂�����Ƃ��ڂɂ�����܂���B�ËL���Ă���e�N�j�b�N���g���ăp���Ɖ����Ă��܂��Ƃ����Q�����ł͂Ȃ��̂ł��B
�Y���̔ԍ���1���炵�č����Ƃ�Ƃ��܂����Ƃ�����܂����A�D�ł͂��܂��s���܂���B
���������ςĂ��ȑQ�����ł́A���������A�Q�����𗘗p���āA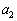 �C
�C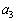 �C������ �Ƌ��߂čs���ƁA���������߂܂��B���܂��s���A��ʍ��̌`���\���ł��āA���Ƃ́A���w�I�A�[�@�ŏؖ�����悢�̂ł��B
�C������ �Ƌ��߂čs���ƁA���������߂܂��B���܂��s���A��ʍ��̌`���\���ł��āA���Ƃ́A���w�I�A�[�@�ŏؖ�����悢�̂ł��B
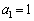 �C
�C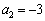 �C
�C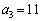 �Ƃ������Ƃ����ɂ킩���Ă���̂ł����A�D���g���āA�ǂ������J���N���ɂȂ��Ă��邩�ׂĂ݂܂��B
�Ƃ������Ƃ����ɂ킩���Ă���̂ł����A�D���g���āA�ǂ������J���N���ɂȂ��Ă��邩�ׂĂ݂܂��B
�D��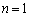 �������Ă݂�ƁA
�������Ă݂�ƁA �D��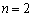 �������Ă݂�̂ł����A
�������Ă݂�̂ł����A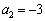 �Ƃ��Ă��܂�Ȃ��ŁA
�Ƃ��Ă��܂�Ȃ��ŁA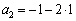 �������܂��B
�������܂��B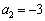 �Ƃ���Ă��܂��ƃJ���N���ɋC�Â��Ȃ���ł��ˁB�Ƃɂ����A���ʂ��o�����A�����o�����A�Ƃ������Ɏv���Ă��܂��ƁA�厖�ȃ|�C���g�������Ă��Ȃ���ł��B
�Ƃ���Ă��܂��ƃJ���N���ɋC�Â��Ȃ���ł��ˁB�Ƃɂ����A���ʂ��o�����A�����o�����A�Ƃ������Ɏv���Ă��܂��ƁA�厖�ȃ|�C���g�������Ă��Ȃ���ł��B ����ł́A�܂������Ă��܂���ˁB
�D��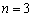 �������Ă݂�ƁA
�������Ă݂�ƁA ���̕ӂŁA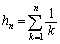 �Ƃ������������A�Ƃ����q���g���g�����Ƃ��l���܂��B
�Ƃ������������A�Ƃ����q���g���g�����Ƃ��l���܂��B
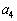 �̑�1����4���Ȃ��A��2����3���Ȃ��A��3����2���Ȃ��A��4���ɂ�1�C2�C3�C4�����ׂđ����Ă���Ƃ����Ƃ��납��A
�̑�1����4���Ȃ��A��2����3���Ȃ��A��3����2���Ȃ��A��4���ɂ�1�C2�C3�C4�����ׂđ����Ă���Ƃ����Ƃ��납��A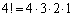 �Ŋ�������ǂ����A�ƁA�l���܂��B����O���ł́A����Ȗ��ł��A���̒��x�̃A�C�f�A���o���A8�������A�����ł��܂��B
�Ŋ�������ǂ����A�ƁA�l���܂��B����O���ł́A����Ȗ��ł��A���̒��x�̃A�C�f�A���o���A8�������A�����ł��܂��B �Ƃ����킯�ł��B����ŁA��ʍ����A
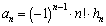 ����E
����E
(i) 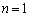 �̂Ƃ��A
�̂Ƃ��A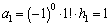 �ƂȂ�A�E�͐��藧���܂��B
�ƂȂ�A�E�͐��藧���܂��B (ii) 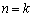 �̂Ƃ��A�E�����藧�Ƃ��āA
�̂Ƃ��A�E�����藧�Ƃ��āA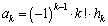
�D�ɑ������ƁA
����āA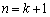 �̂Ƃ����E�����藧���܂��B
�̂Ƃ����E�����藧���܂��B (i)�C(ii)���A�S�Ă̎��R��n�ɂ��āA�E�����藧���܂��B
����āA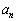 �C
�C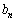 �̈�ʍ��́A
�̈�ʍ��́A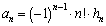 �C
�C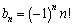 ......[��]
......[��]
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���嗝�n���wTOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B