���嗝�n���w'07�N�O��[4]
�ȉ��̖₢�ɓ�����B
(1) ����a�ɑ��A2���̐����s��A�CP�CQ���A5�̏���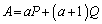 �C
�C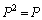 �C
�C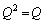 �C
�C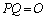 �C
�C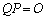 ���݂����Ƃ���B������
���݂����Ƃ���B������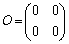 �ł���B���̂Ƃ��A
�ł���B���̂Ƃ��A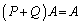 �����藧���Ƃ������B
�����藧���Ƃ������B (2) a�͐��̐��Ƃ��āA�s��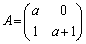 ���l����B����A�ɑ��A(1)��5�̏��������ׂĂ݂����s��P�CQ�����߂�B
���l����B����A�ɑ��A(1)��5�̏��������ׂĂ݂����s��P�CQ�����߂�B (3) n��2�ȏ�̐����Ƃ��A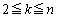 ���݂�������k�ɑ���
���݂�������k�ɑ���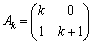 �Ƃ����B�s��̐�
�Ƃ����B�s��̐�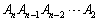 �����߂�B
�����߂�B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@���吔�w�ł͓����Z�I�Ȃǒʗp���Ȃ��A�Ƃ����̂��A���̎��_�ł����A����������������ƁA���嗝�n��ڎw���̂ł���A���Ԃŗ��ʂ��Ă�������Z�I�͈�ʂ�}�X�^�[���Ă��ē��R�A�ƌ������Ƃ��ł���̂ł��B
�@���̑O��m�����Ȃ��A�s��̒�`�Ɗ�{�I�Ȍv�Z����(�s�����Q��)��m���Ă��邾���ł��A���̖��̉��������Ƃ��ł��܂����A�X�y�N�g��������m���Ă���A���̖��̉�10���������炸�ɑ����ɏ����������Ƃ��ł��܂��B
�@��蕶��5�̏��������āAP�CQ��A�̎ˉe�q�Ƃ��Ă̐����������Ă���(�u�X�y�N�g�������v�A�u�ˉe�q�v�Ƃ����p��́A�ŗL�x�N�g�����������Ă���悤�ȂƂ��Ɏg���̂ŁA���̖��ł͐��m�ɂ͎ˉe�q�ł͂���܂���)�Ƃ������Ƃ͒m���̂���l�Ȃ�ꌩ���Ă킩���Ă��܂��܂��B����ƁA���̉��l�b�g��ɏo�������Œ��쌠�N�Q�ƌ���ꂩ�˂Ȃ��ȂƎv�����炢�ɁA���Ƃ͈�{���ł��B�킴�킴�A����ȑO�u���������Ă���̂��A���쌠��A�Ƃ������ƂŁA�X�y�N�g�������ɂ��Ēm��������Ƃ����O��ōl���Ă����܂��B
(2) 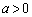 ���A
���A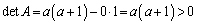
�]���āA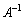 �����݂��܂��B(�t�s�����Q��)
�����݂��܂��B(�t�s�����Q��)
(1)�Ŏ����������ӂ̉E������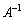 �������āA
�������āA �� 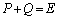 �@����@�@(E��2���̒P�ʍs��)��蕶�ŗ^����ꂽ�����F
�@����@�@(E��2���̒P�ʍs��)��蕶�ŗ^����ꂽ�����F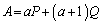 �@����A
�@����A
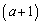 �~�@�|�A���A
�~�@�|�A���A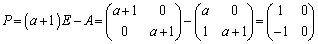
�A�|a�~�@���A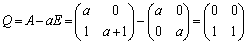 ......[��]
......[��]
(3) 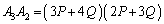
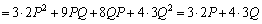 �@����B
�@����B���A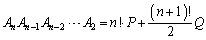 �Ɨ\���ł��܂��B���w�I�A�[�@�ɂ���ė\�������������Ƃ������܂��B
�Ɨ\���ł��܂��B���w�I�A�[�@�ɂ���ė\�������������Ƃ������܂��B (I) 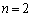 �̂Ƃ��A�A���
�̂Ƃ��A�A���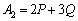 �C����ė\���͐��������Ƃ��킩��܂��B
�C����ė\���͐��������Ƃ��킩��܂��B (II) 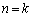 �̂Ƃ��\�����������Ƃ��āA
�̂Ƃ��\�����������Ƃ��āA �����藧���܂��B
���ӂɁA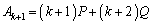 �������炩����ƁA
�������炩����ƁA ����āA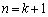 �̂Ƃ��ɂ��\���͐��������Ƃ������܂��B
�̂Ƃ��ɂ��\���͐��������Ƃ������܂��B (I)�C(II)���A�\����n��2�ȏ�̐����̂Ƃ����������Ƃ������܂����B
�����p���āA
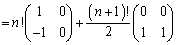
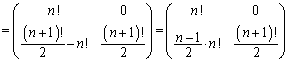 ......[��]
......[��]
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���嗝�n���wTOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B 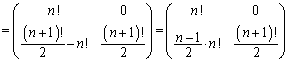 ......[��]
......[��]