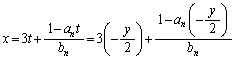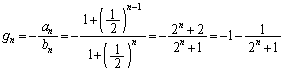���嗝�n���w'08�N�O��[1]
���W���ʂ̓_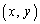 ��
��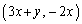 �ֈڂ��ړ�f���l���A�_P�̈ڂ�s�����
�ֈڂ��ړ�f���l���A�_P�̈ڂ�s�����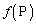 �ƕ\���Bf��p���Ē���
�ƕ\���Bf��p���Ē���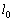 �C
�C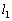 �C
�C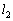 �C��� ���ȉ��̂悤�ɒ�߂�B
�C��� ���ȉ��̂悤�ɒ�߂�B
�E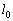 �͒���
�͒���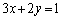 �ł���B
�ł���B �E�_P��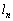 ����Ƃ��A
����Ƃ��A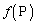 ���`��������
���`��������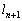 �Ƃ���(
�Ƃ���(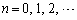 )�B
)�B �ȉ�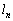 ��1�����p����
��1�����p����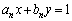 �ƕ\���B
�ƕ\���B
(2) �s����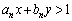 ����߂�̈��
����߂�̈��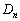 �Ƃ���B
�Ƃ���B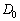 �C
�C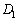 �C
�C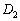 �C��� ���ׂĂɊ܂܂��悤�ȓ_�͈̔͂�}������B
�C��� ���ׂĂɊ܂܂��悤�ȓ_�͈̔͂�}������B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@(2)�́A���������Ė����p�`�H�Ǝv������A��┏�q�����ł����B
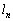 �F
�F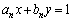 ��̓_���ړ�f�ɂ���āA�ǂ������_�Ɉړ�����̂����l���A�ړ���̓_������Ă��钼��
��̓_���ړ�f�ɂ���āA�ǂ������_�Ɉړ�����̂����l���A�ړ���̓_������Ă��钼��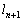 �����߂Ă݂܂��B
�����߂Ă݂܂��B
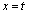 �Ƃ�
�Ƃ�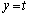 �Ƃ������ƂɂȂ�܂����A
�Ƃ������ƂɂȂ�܂����A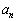 ��
��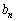 ��0�̏ꍇ�ɂ͍��邱�Ƃ��N����̂ŁA�ʈ����ɂ��čl���邱�Ƃɂ��܂��B
��0�̏ꍇ�ɂ͍��邱�Ƃ��N����̂ŁA�ʈ����ɂ��čl���邱�Ƃɂ��܂��B
�܂��A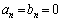 �ł́A
�ł́A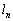 �������ɂȂ�܂���B
�������ɂȂ�܂���B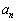 ��
��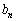 �̂ǂ��炩�����0�ɂȂ�܂���B�����ŁA
�̂ǂ��炩�����0�ɂȂ�܂���B�����ŁA(i) 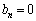 �̂Ƃ��A
�̂Ƃ��A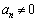 �C
�C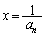 �C
�C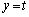 �Ƃ����AP
�Ƃ����AP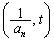 �Ƃ��āA����t�����낢��Ȓl���Ƃ�Ƃ��A
�Ƃ��āA����t�����낢��Ȓl���Ƃ�Ƃ��A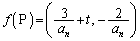 �́A����
�́A����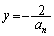 ��`���܂��B
��`���܂��B 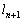 �F
�F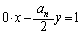
���A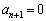 �C
�C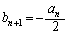 �@����@
�@����@ (ii) 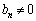 �̂Ƃ��A
�̂Ƃ��A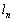 ��
��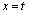 �Ƃ���ƁA
�Ƃ���ƁA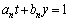 �C
�C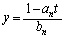 �C
�C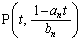 �Ƃ��āA
�Ƃ��āA �����ŁA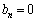 �Ƃ���ƁA�@�ƈ�v����̂ŁA(i)�C(ii)���킹�āA
�Ƃ���ƁA�@�ƈ�v����̂ŁA(i)�C(ii)���킹�āA
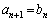 �C
�C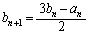 ......[��]
......[��]
(2) (1)���A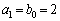 �C
�C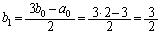
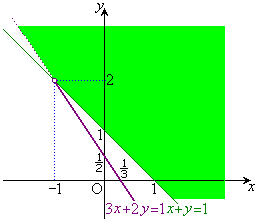
�������āA��������̒������ł���킯�ł����A�����ɑ��݂��钼���ň͂ސ}�`���Ƃ���ƁA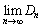 �������p�`�ɂȂ肩�˂܂���B
�������p�`�ɂȂ肩�˂܂���B
�����ŁA�����̒������ǂ̂悤�Ɍ�_����邩�ׂ܂��B
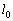 �F
�F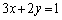 �ƁA
�ƁA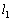 �F
�F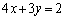 ��A������ƁA
��A������ƁA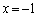 �C
�C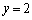 �ƂȂ�܂��B
�ƂȂ�܂��B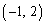 ��f�ɂ���āA�ǂ��Ɉڂ邩�ׂ܂��B
��f�ɂ���āA�ǂ��Ɉڂ邩�ׂ܂��B �ƂȂ��āA�������g�Ɉڂ�܂��B
�Ƃ������Ƃ́A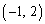 ��
��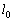 ��
��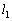 �̌�_�ł���ƂƂ��ɁA
�̌�_�ł���ƂƂ��ɁA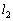 ��̓_�ł�����A�J��Ԃ�f�ɂ���Ĉړ�������ƁA�S�Ă�n�ɂ��āA
��̓_�ł�����A�J��Ԃ�f�ɂ���Ĉړ�������ƁA�S�Ă�n�ɂ��āA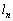 ��̓_���Ƃ������Ƃł��B
��̓_���Ƃ������Ƃł��B
����������ƁA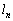 �͑S��
�͑S��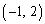 ��ʂ�A�Ƃ������Ƃł��B
��ʂ�A�Ƃ������Ƃł��B
�ł���A�̈�����߂邽�߂ɂ́A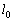 �C
�C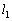 �C
�C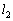 �C��� �̒��ŁA�X�����ő�̒����ƍŏ��̒��������߂�悢���ƂɂȂ�܂�(�s�����Ɨ̈����Q��)�B(1)�̌��ʂ��A
�C��� �̒��ŁA�X�����ő�̒����ƍŏ��̒��������߂�悢���ƂɂȂ�܂�(�s�����Ɨ̈����Q��)�B(1)�̌��ʂ��A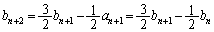
�����������́A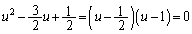
�� 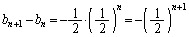 �@����C
�@����C �B�|�C���A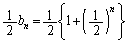
 ����
����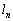 �̌X���́A
�̌X���́A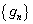 �͒P�������Ȑ���ŁA
�͒P�������Ȑ���ŁA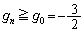
�܂��A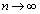 �̂Ƃ��A
�̂Ƃ��A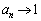 �C
�C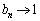 �C
�C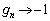 �ŁA
�ŁA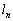 �͒����F
�͒����F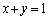 �ɋ߂Â��܂��B�߂Â��܂����A
�ɋ߂Â��܂��B�߂Â��܂����A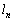 ��
��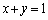 �Ɉ�v����킯�ł͂Ȃ��̂ŁA
�Ɉ�v����킯�ł͂Ȃ��̂ŁA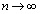 �ł����Ă��A
�ł����Ă��A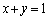 ����
����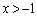 �̕����́A
�̕����́A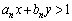 �Ƃ����̈�Ɋ܂܂�܂��B
�Ƃ����̈�Ɋ܂܂�܂��B
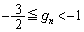 ���A
���A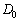 �C
�C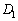 �C
�C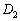 �C��� ���ׂĂɊ܂܂��悤�ȓ_�͈̔͂́A�E�}�ʼn��ΐF�ɒ��F��������(����
�C��� ���ׂĂɊ܂܂��悤�ȓ_�͈̔͂́A�E�}�ʼn��ΐF�ɒ��F��������(����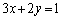 ��(�_���A�y�сA���}��)���܂܂��A����
��(�_���A�y�сA���}��)���܂܂��A����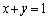 ���
���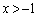 �̕���(����)���܂�)�B
�̕���(����)���܂�)�B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���嗝�n���wTOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B