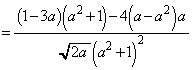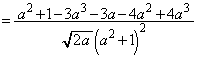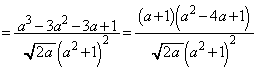東大理系数学'11年前期[1]
座標平面において、点P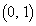 を中心とする半径1の円をCとする。aを
を中心とする半径1の円をCとする。aを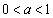 を満たす実数とし、直線
を満たす実数とし、直線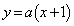 とCとの交点をQ,Rとする。
とCとの交点をQ,Rとする。
(1) △PQRの面積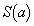 を求めよ。
を求めよ。 (2) aが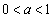 の範囲を動くとき、
の範囲を動くとき、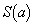 が最大となるaを求めよ。
が最大となるaを求めよ。
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
解答 弦の長さを、点と直線の距離の公式から考える標準的な最大・最小問題です。
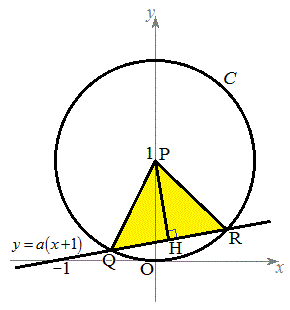 (1)
(1) 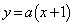 は、
は、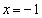 とすると、aの値にかかわらず
とすると、aの値にかかわらず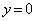 となるので、定点
となるので、定点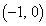 を通り傾きaの直線を表します(定点を通る直線を参照)。
を通り傾きaの直線を表します(定点を通る直線を参照)。点P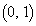 から直線
から直線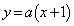 ,つまり、
,つまり、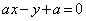 に下ろした垂線PHの長さは、
に下ろした垂線PHの長さは、 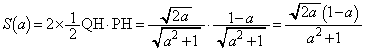 ......[答]
......[答]
(2) 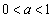 のとき、
のとき、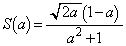
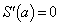 とすると、
とすると、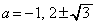 (
(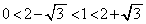 )
)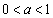 の範囲で増減表は(関数の増減を参照)、これより、
の範囲で増減表は(関数の増減を参照)、これより、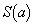 を最大とするaは、
を最大とするaは、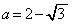 ......[答]
......[答]
追記.(1)のPHをaの関数とみて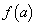 とすると、
とすると、 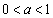 において、
において、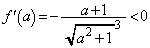 より、
より、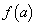 は減少関数で、
は減少関数で、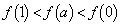 です。これより、
です。これより、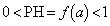 となります。
となります。
従って、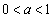 のとき、直線と円は必ず2交点をもちます(図形的に明らかですが)。
のとき、直線と円は必ず2交点をもちます(図形的に明らかですが)。
また、(2)では、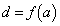 (
(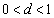 )とおくと、
)とおくと、より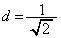 (
(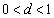 を満たす)のとき
を満たす)のとき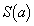 最大となりますが、このとき、
最大となりますが、このとき、 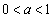 より、
より、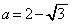 となります。
となります。
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
東大理系数学TOP 数学TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2024(有)りるらる 苦学楽学塾 随時入会受付中!理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。 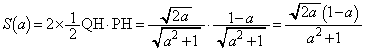 ......[答]
......[答]