���嗝�n���w'18�N�O��[2]
����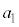 �C
�C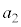 �C�������C��
�C�������C��
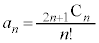 (
(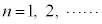 )
)
(1) 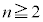 �Ƃ���B
�Ƃ���B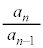 ������
������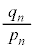 �Ƃ��ĕ\�����Ƃ��̕���
�Ƃ��ĕ\�����Ƃ��̕���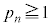 �ƕ��q
�ƕ��q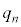 �����߂�B
�����߂�B (2) 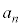 �������ƂȂ�
�������ƂȂ�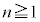 �����ׂċ��߂�B
�����ׂċ��߂�B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@�{��ł́A�V���~�Ԃ��Ŏ������ԓ��ɏ[���ɉł��܂��B�Ȃ��A�����A�g�ݍ��킹���Q�Ƃ��Ă��������B
(1) 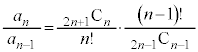

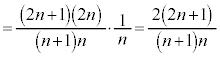 �@����@
�@����@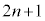 ��
��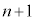 ������d(
������d( )�����Ƃ���ƁAk�Cl�𐮐��Ƃ��āA
)�����Ƃ���ƁAk�Cl�𐮐��Ƃ��āA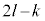 �͐����Ȃ̂ŁA
�͐����Ȃ̂ŁA �Ɍ����A����́A
�Ɍ����A����́A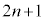 ��
��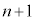 ���݂��ɑf�ł��邱�Ƃ��Ӗ����܂��B
���݂��ɑf�ł��邱�Ƃ��Ӗ����܂��B
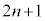 ��n������d(
��n������d(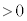 )�����Ƃ���ƁAk�Cl�𐮐��Ƃ��āA
)�����Ƃ���ƁAk�Cl�𐮐��Ƃ��āA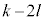 �͐����Ȃ̂ŁA
�͐����Ȃ̂ŁA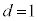 �Ɍ����A����́A
�Ɍ����A����́A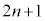 ��n���݂��ɑf�ł��邱�Ƃ��Ӗ����܂��B
��n���݂��ɑf�ł��邱�Ƃ��Ӗ����܂��B
����āA�@�̂����A���q�� �ƕ����
�ƕ����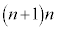 �݂͌��ɑf�ł��B�܂��An��
�݂͌��ɑf�ł��B�܂��An��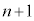 �̂����ꂩ����͋����Ȃ̂ŁA
�̂����ꂩ����͋����Ȃ̂ŁA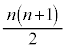 �͐����ł���A
�͐����ł���A �ƌ݂��ɑf�ł��B����āA
�ƌ݂��ɑf�ł��B����āA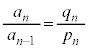 �ƂȂ����
�ƂȂ����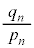 �C�����A�݂��ɑf�Ȏ��R���̑g
�C�����A�݂��ɑf�Ȏ��R���̑g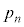 �C
�C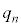 �́A
�́A
�Ƃ���Ă����ƁA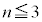 �ł�
�ł� �ł����A
�ł����A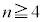 �ł�
�ł�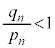 �ɂȂ肻���ł��B�܂��A������m���߂܂��B
�ɂȂ肻���ł��B�܂��A������m���߂܂��B ����āA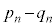 �́A
�́A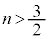 �ɂ����Ă͒P�������ŁA
�ɂ����Ă͒P�������ŁA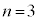 �̂Ƃ��́A
�̂Ƃ��́A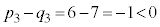 �ł����A
�ł����A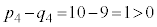 �ŁA
�ŁA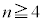 �ɂ����ẮA
�ɂ����ẮA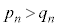 �@����B
�@����B
�ł��B����A�A�ɂ��ƁA �ƂȂ�܂����A�B���A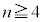 �ł́A
�ł́A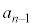 �ɂ����鐔
�ɂ����鐔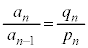 ��1��菬�����Ȃ�̂ŁA
��1��菬�����Ȃ�̂ŁA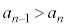 �ɂȂ�܂��B�����ŁAn������ɑ傫�����Ȃ���
�ɂȂ�܂��B�����ŁAn������ɑ傫�����Ȃ���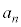 ���ǂ��Ȃ邩���ׂĂ݂܂��B
���ǂ��Ȃ邩���ׂĂ݂܂��B ��L�ł͒��ځA��`���F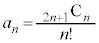 ��p���Čv�Z���܂������A
��p���Čv�Z���܂������A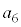 ����v�Z����Ȃ�Q�����@��p��������悢�Ǝv���܂��B��L�ł́A
����v�Z����Ȃ�Q�����@��p��������悢�Ǝv���܂��B��L�ł́A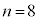 ��
��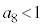 �ɂȂ�܂������A���ɂȂ��Ȃ����ʂ����������A�r����
�ɂȂ�܂������A���ɂȂ��Ȃ����ʂ����������A�r����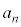 ���璲�ׂ�̂ł���A��`�����g��Ȃ���Ȃ�܂���B��`�����g������
���璲�ׂ�̂ł���A��`�����g��Ȃ���Ȃ�܂���B��`�����g������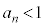 �ƂȂ�n��������A�Ƃ����ۏ͂���܂��A������Ȃ��Ȃ�A�ʂ̂��Ƃ��l���Ȃ���Ȃ�܂���B
�ƂȂ�n��������A�Ƃ����ۏ͂���܂��A������Ȃ��Ȃ�A�ʂ̂��Ƃ��l���Ȃ���Ȃ�܂���B
�Ƃ�������L���A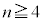 �ł́A
�ł́A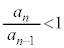 �ł���A
�ł���A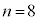 �ɂ�����
�ɂ�����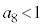 �Ȃ̂ŁA
�Ȃ̂ŁA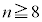 �ɂ�����
�ɂ����� �ł���A
�ł���A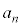 �������ɂȂ邱�Ƃ͂���܂���B
�������ɂȂ邱�Ƃ͂���܂���B
 �ɂ�����
�ɂ����� �������ɂȂ�̂́A�C�C
�������ɂȂ�̂́A�C�C �C
�C ���A
���A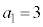 �C
�C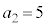 �݂̂ł��B
�݂̂ł��B
����āA �������ƂȂ�
�������ƂȂ�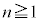 �́A
�́A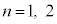 ......[��]
......[��]
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���嗝�n���wTOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B 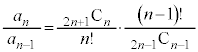

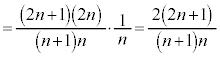 �@����@
�@����@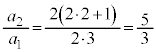 �C
�C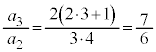 �C
�C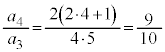 �C
�C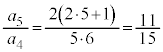 �@����A
�@����A