東京大学理系2018年前期数学入試問題
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
[1] 関数
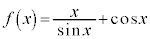 (
(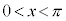 )
)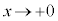 ,
,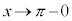 のときの極限を調べよ。
のときの極限を調べよ。
[解答へ]
[2] 数列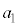 ,
,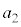 ,・・・・・・,を
,・・・・・・,を
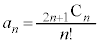 (
(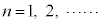 )
)
(1) 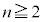 とする。
とする。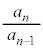 を既約分数
を既約分数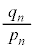 として表したときの分母
として表したときの分母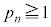 と分子
と分子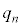 を求めよ。
を求めよ。 (2) 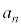 が整数となる
が整数となる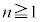 をすべて求めよ。
をすべて求めよ。 [解答へ]
[3] 放物線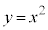 のうち
のうち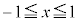 をみたす部分をCとする。座標平面上の原点Oと点A
をみたす部分をCとする。座標平面上の原点Oと点A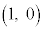 を考える。
を考える。
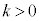 を実数とする。点PがC上を動き、点Qが線分OA上を動くとき、
を実数とする。点PがC上を動き、点Qが線分OA上を動くとき、
をみたす点Rが動く領域の面積を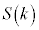 とする。
とする。
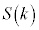 および
および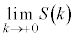 ,
,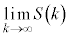 を求めよ。
を求めよ。
[解答へ]
[4] 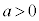 とし、
とし、
とおく。次の2条件をみたす点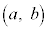 の動きうる範囲を求め、座標平面上に図示せよ。
の動きうる範囲を求め、座標平面上に図示せよ。
条件1:方程式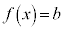 は相異なる3実数解をもつ。
は相異なる3実数解をもつ。 [解答へ]
[5] 複素数平面上の原点を中心とする半径1の円をCとする。点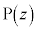 はC上にあり、点
はC上にあり、点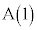 とは異なるとする。点Pにおける円Cの接線に関して、点Aと対称な点を
とは異なるとする。点Pにおける円Cの接線に関して、点Aと対称な点を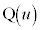 とする。
とする。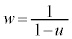 とおき、wと共役な複素数を
とおき、wと共役な複素数を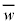 で表す。
で表す。
(1) uと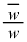 をzについての整式として表し、絶対値の商
をzについての整式として表し、絶対値の商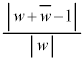 を求めよ。
を求めよ。 (2) Cのうち実部が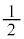 以下の複素数で表される部分を
以下の複素数で表される部分を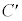 とする。点
とする。点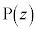 が
が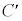 上を動くときの点
上を動くときの点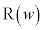 の軌跡を求めよ。
の軌跡を求めよ。 [解答へ]
[6] 座標空間内の4点O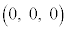 ,A
,A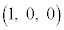 ,B
,B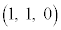 ,C
,C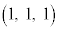 を考える。
を考える。
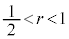 とする。点Pが線分OA,AB,BC上を動くときに点Pを中心とする半径rの球(内部を含む)が通過する部分を、それぞれ
とする。点Pが線分OA,AB,BC上を動くときに点Pを中心とする半径rの球(内部を含む)が通過する部分を、それぞれ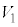 ,
,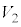 ,
,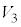 とする。
とする。
(1) 平面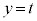 が
が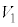 ,
,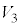 双方と共有点をもつようなt の範囲を与えよ。さらに、この範囲のt に対し、平面
双方と共有点をもつようなt の範囲を与えよ。さらに、この範囲のt に対し、平面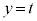 と
と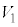 の共通部分および、平面
の共通部分および、平面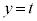 と
と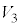 の共通部分を同一平面上に図示せよ。
の共通部分を同一平面上に図示せよ。 (2) 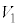 と
と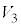 の共通部分が
の共通部分が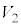 に含まれるためのrについての条件を求めよ。
に含まれるためのrについての条件を求めよ。 (3) rは(2)の条件をみたすとする。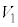 の体積をSとし、
の体積をSとし、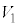 と
と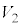 の共通部分の体積をTとする。
の共通部分の体積をTとする。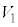 ,
,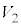 ,
,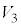 を合わせて得られる立体Vの体積をSとTを用いて表せ。
を合わせて得られる立体Vの体積をSとTを用いて表せ。 (4) ひきつづきrは(2)の条件をみたすとする。SとTを求め、Vの体積を決定せよ。
[解答へ]
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
東大理系数学TOP 数学TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2025(有)りるらる 苦学楽学塾 随時入会受付中!理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。 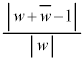 を求めよ。
を求めよ。