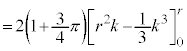���嗝�n���w'18�N�O��[6]
���W��ԓ���4�_O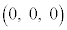 �CA
�CA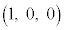 �CB
�CB �CC
�CC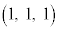 ���l����B
���l����B
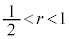 �Ƃ���B�_P������OA�CAB�CBC����Ƃ��ɓ_P�𒆐S�Ƃ��锼�ar�̋�(�������܂�)���ʉ߂��镔�����A���ꂼ��
�Ƃ���B�_P������OA�CAB�CBC����Ƃ��ɓ_P�𒆐S�Ƃ��锼�ar�̋�(�������܂�)���ʉ߂��镔�����A���ꂼ��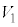 �C
�C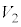 �C
�C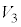 �Ƃ���B
�Ƃ���B
(1) ���� ��
��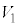 �C
�C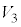 �o���Ƌ��L�_�����悤��t �͈̔͂�^����B����ɁA���͈̔͂�t �ɑ��A����
�o���Ƌ��L�_�����悤��t �͈̔͂�^����B����ɁA���͈̔͂�t �ɑ��A���� ��
��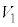 �̋��ʕ�������сA����
�̋��ʕ�������сA����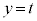 ��
��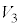 �̋��ʕ����ꕽ�ʏ�ɐ}������B
�̋��ʕ����ꕽ�ʏ�ɐ}������B (2) 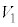 ��
��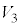 �̋��ʕ�����
�̋��ʕ�����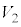 �Ɋ܂܂�邽�߂�r�ɂ��Ă̏��������߂�B
�Ɋ܂܂�邽�߂�r�ɂ��Ă̏��������߂�B (3) r��(2)�̏������݂����Ƃ���B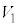 �̑̐ς�S�Ƃ��A
�̑̐ς�S�Ƃ��A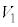 ��
��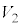 �̋��ʕ����̑̐ς�T�Ƃ���B
�̋��ʕ����̑̐ς�T�Ƃ���B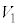 �C
�C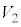 �C
�C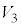 �����킹�ē����闧��V�̑̐ς�S��T��p���ĕ\���B
�����킹�ē����闧��V�̑̐ς�S��T��p���ĕ\���B (4) �Ђ��Â�r��(2)�̏������݂����Ƃ���BS��T�����߁AV�̑̐ς����肹��B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@ �{�N��3���������ł������A�{����ʉߗ̈���ڍׂɑ���ɂ���Ɣj�]���܂��B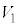 �C
�C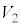 �C
�C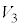 �͔����̊Ԃɉ~�������܂������̂ł��邱�Ƃ͖��炩�Ȃ̂ŁA�ו��ɂ͗������炸�A�T�������������x�ŁA�̐ς̌v�Z�Ɉڂ�ׂ��ł��B
�͔����̊Ԃɉ~�������܂������̂ł��邱�Ƃ͖��炩�Ȃ̂ŁA�ו��ɂ͗������炸�A�T�������������x�ŁA�̐ς̌v�Z�Ɉڂ�ׂ��ł��B
�_P�𒆐S�Ƃ��锼�ar�����ʂ̕��������AP��OA��AAB��ABC��ɂ���ꍇ�ɕ����ď����ƈȉ��̂悤�ɂȂ�܂��B
P��OA���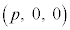 �ɂ���Ƃ��̋��ʂ�
�ɂ���Ƃ��̋��ʂ�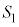 �Ƃ��āA
�Ƃ��āA
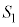 �F
�F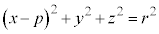 �@����@
�@����@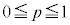 �͈̔͂ŕω�����Ƃ��A
�͈̔͂ŕω�����Ƃ��A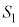 �Ƃ��̓������ʉ߂��镔����
�Ƃ��̓������ʉ߂��镔����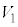 �ł��B
�ł��B
P��AB���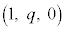 �ɂ���Ƃ��̋��ʂ�
�ɂ���Ƃ��̋��ʂ� �Ƃ��āA
�Ƃ��āA
 �F
�F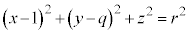 �@����A
�@����A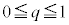 �͈̔͂ŕω�����Ƃ��A
�͈̔͂ŕω�����Ƃ��A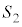 �Ƃ��̓������ʉ߂��镔����
�Ƃ��̓������ʉ߂��镔����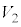 �ł��B
�ł��B
P��BC���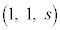 �ɂ���Ƃ��̋��ʂ�
�ɂ���Ƃ��̋��ʂ�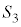 �Ƃ��āA
�Ƃ��āA
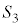 �F
�F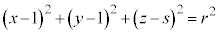 �@����B
�@����B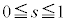 �͈̔͂ŕω�����Ƃ��A
�͈̔͂ŕω�����Ƃ��A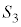 �Ƃ��̓������ʉ߂��镔����
�Ƃ��̓������ʉ߂��镔���� �ł��B
�ł��B
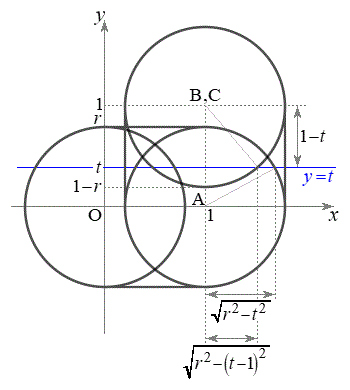 ������xy���ʂ̏�����璭�߂��Ƃ��̐}���E�}�Ɏ����܂��BB�CC�͏d�Ȃ��Č����܂��B
������xy���ʂ̏�����璭�߂��Ƃ��̐}���E�}�Ɏ����܂��BB�CC�͏d�Ȃ��Č����܂��B
(1) ����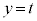 (�E�}��)��ł́A
(�E�}��)��ł́A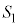 �̒f�ʂɂł���~�́A�@��
�̒f�ʂɂł���~�́A�@��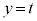 �Ƃ���(�~�̕��������Q��)�A
�Ƃ���(�~�̕��������Q��)�A
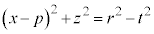 (
(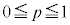 )�@����C
)�@����C���̉~�����݂��邽�߂ɁA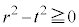 �C�܂�A
�C�܂�A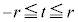 �@����D
�@����D
���̂Ƃ��A����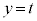 ��
��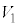 �Ƌ��L�_�������܂��B
�Ƌ��L�_�������܂��B
����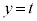 ��ł́A
��ł́A �̒f�ʂɂł���~�́A�B��
�̒f�ʂɂł���~�́A�B��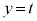 �Ƃ��āA
�Ƃ��āA 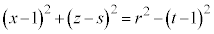
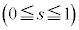 �@����E
�@����E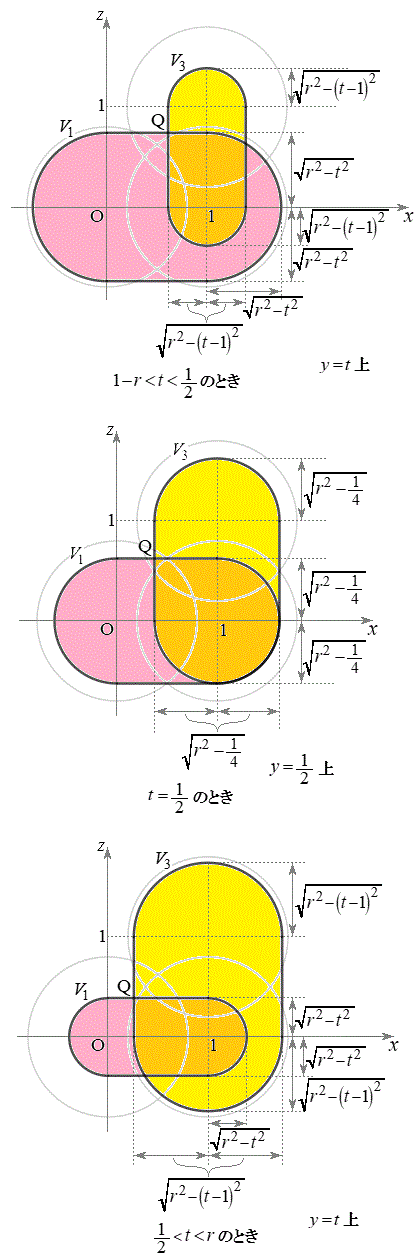 �E����
�E����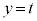 ��
��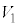 �Ƃ̋��ʕ����́A�C��
�Ƃ̋��ʕ����́A�C�� �̂Ƃ���
�̂Ƃ���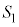 �̒f�ʂɂł���~�F
�̒f�ʂɂł���~�F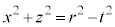 �̂���
�̂���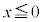 �̕����̔��~�ƁA�C��
�̕����̔��~�ƁA�C��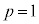 �̂Ƃ���
�̂Ƃ���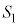 �̒f�ʂɂł���~�F
�̒f�ʂɂł���~�F �̂���
�̂���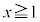 �̕����̔��~�ɋ��܂ꂽ�����ŁA
�̕����̔��~�ɋ��܂ꂽ�����ŁA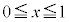 �ɂ����Ă͇C��
�ɂ����Ă͇C��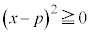 ���
���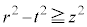 �C�����A
�C�����A
�ł��B�E�}(����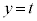 �Ő����f��)�Ńs���N�F�̕����ƞ�F�̕��������킹���̈�ɂȂ�܂��B
�Ő����f��)�Ńs���N�F�̕����ƞ�F�̕��������킹���̈�ɂȂ�܂��B �E����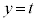 ��
�� �̋��ʕ����́A�E��
�̋��ʕ����́A�E��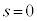 �̂Ƃ���
�̂Ƃ���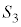 �̒f�ʂɂł���~�F
�̒f�ʂɂł���~�F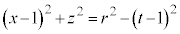 �̂���
�̂���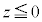 �̕����̔��~�ƁA�E��
�̕����̔��~�ƁA�E��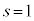 �̂Ƃ���
�̂Ƃ���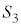 �̒f�ʂ��ł���~�F
�̒f�ʂ��ł���~�F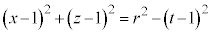 �̂���
�̂���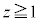 �̕����ɂł��锼�~�ɋ��܂ꂽ�����ŁA
�̕����ɂł��锼�~�ɋ��܂ꂽ�����ŁA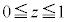 �ɂ����Ă͇E��
�ɂ����Ă͇E��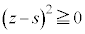 ���
���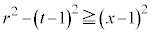 �C�����A
�C�����A �ł��B�E�}�ʼn��F�̕����ƞ�F�̕��������킹���̈�ɂȂ�܂��B
�������A
�E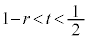 �ł́A
�ł́A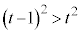 ��
��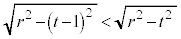 �C
�C �̒f�ʂ̔��~�̕���
�̒f�ʂ̔��~�̕��� �̒f�ʂ̔��~�������a���傫���Ȃ�܂��B
�̒f�ʂ̔��~�������a���傫���Ȃ�܂��B �E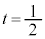 �ł́A
�ł́A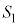 �̒f�ʂ̔��~��
�̒f�ʂ̔��~��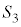 �̒f�ʂ̔��~�̔��a�͓������Ȃ�܂��B
�̒f�ʂ̔��~�̔��a�͓������Ȃ�܂��B �E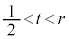 �ł́A
�ł́A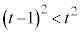 ��
��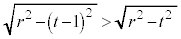 �C
�C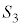 �̒f�ʂ̔��~�̕���
�̒f�ʂ̔��~�̕��� �̒f�ʂ̔��~�������a���傫���Ȃ�܂��B
�̒f�ʂ̔��~�������a���傫���Ȃ�܂��B �ȏ���A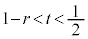 �C
�C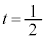 �C
�C �̏ꍇ�ɕ����āA����
�̏ꍇ�ɕ����āA����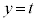 ��
��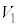 �̋��ʕ�������сA����
�̋��ʕ�������сA����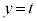 ��
��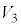 �̋��ʕ����ꕽ�ʏ�ɐ}������ƁA�E�}�̂悤�ɂȂ�܂��B���F���F���ƞ�F���F�������킹���̈悪
�̋��ʕ����ꕽ�ʏ�ɐ}������ƁA�E�}�̂悤�ɂȂ�܂��B���F���F���ƞ�F���F�������킹���̈悪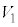 �����A���F���F���ƞ�F���F�������킹���̈悪
�����A���F���F���ƞ�F���F�������킹���̈悪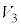 �����A��F���F����
�����A��F���F����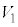 ��
��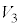 �̋��ʕ����ł��B
�̋��ʕ����ł��B
(2) ����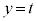 ���
���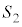 �̒f�ʂɂł���~�́A���̒��S��
�̒f�ʂɂł���~�́A���̒��S��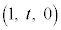 �ł����āA�A��
�ł����āA�A��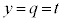 (
(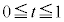 )�Ƃ��āA
)�Ƃ��āA 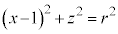 �@����G
�@����G�ł��B
���āA(1)�̗̈��}������ƁA����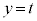 ��ŁA
��ŁA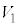 �C
�C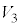 �̋��ʕ���(�E�}��F���F��)���A�G�̉~((1)�̐}�ł́A(1,???t,???0)�𒆐S�Ƃ��锼�ar�̉~�A�����D�F�ŕ`����Ă��܂�)�̊O�ɏo�Ă��܂��\�������邱�Ƃ��킩��܂��B���ʕ����̂����~�̒��S
�̋��ʕ���(�E�}��F���F��)���A�G�̉~((1)�̐}�ł́A(1,???t,???0)�𒆐S�Ƃ��锼�ar�̉~�A�����D�F�ŕ`����Ă��܂�)�̊O�ɏo�Ă��܂��\�������邱�Ƃ��킩��܂��B���ʕ����̂����~�̒��S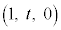 ����ł������_Q�̍��W�́A
����ł������_Q�̍��W�́A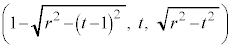 �ł��B(1)���A
�ł��B(1)���A ��
��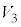 �̋��ʕ��������݂���̂́A
�̋��ʕ��������݂���̂́A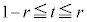 �̂Ƃ��ł����A
�̂Ƃ��ł����A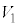 ��
��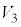 �̋��ʕ�����
�̋��ʕ�����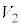 �Ɋ܂܂�邽�߂ɂ́A�_Q���~�G�Ɋ܂܂�邱�Ƃ������ŁA���̂��߂ɂ́AQ�Ɖ~�̒��S
�Ɋ܂܂�邽�߂ɂ́A�_Q���~�G�Ɋ܂܂�邱�Ƃ������ŁA���̂��߂ɂ́AQ�Ɖ~�̒��S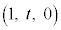 �Ƃ̋��������a�ȉ��ł���悭�A
�Ƃ̋��������a�ȉ��ł���悭�A 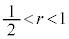 �Ȃ̂ŁA
�Ȃ̂ŁA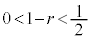 �C����ćH�E�ӂ�t ��2�����̎��ɂ���
�C����ćH�E�ӂ�t ��2�����̎��ɂ���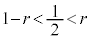 �Ȃ̂ŁA�H�E�ӂ�
�Ȃ̂ŁA�H�E�ӂ�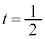 �̂Ƃ��ŏ��l
�̂Ƃ��ŏ��l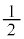 ���Ƃ�C�H��
���Ƃ�C�H��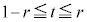 �̂��ׂĂ�t �Ő������邽�߂ɂ�
�̂��ׂĂ�t �Ő������邽�߂ɂ�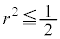 ����
����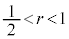 �C����āA
�C����āA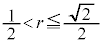 ......[��]
......[��]
 (3)
(3)  �C
�C �C
�C �̑̐ς͂������S�ł��B
�̑̐ς͂������S�ł��B �C
�C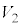 �C
�C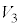 �����킹�ē����闧�̂̑̐ς́A
�����킹�ē����闧�̂̑̐ς́A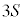 ����
����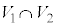 �C
�C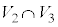 �C
�C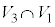 �̑̐ς������A
�̑̐ς������A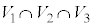 �̑̐ς����������̂ɂȂ�܂��B(2)�̏�������������Ă���
�̑̐ς����������̂ɂȂ�܂��B(2)�̏�������������Ă���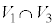 ��
��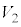 �Ɋ܂܂�Ă��܂��̂ŁA
�Ɋ܂܂�Ă��܂��̂ŁA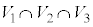 �̑̐ς�
�̑̐ς�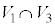 �̑̐ς͓������Ȃ�܂��B�܂��A
�̑̐ς͓������Ȃ�܂��B�܂��A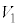 ��
��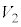 �̈ʒu�W�ƁA
�̈ʒu�W�ƁA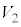 ��
��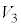 �̈ʒu�W�͓������A
�̈ʒu�W�͓������A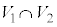 ��
��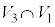 �̑̐ς͂Ƃ���T�ł��B
�̑̐ς͂Ƃ���T�ł��B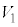 �C
�C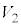 �C
�C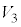 �����킹�ē����闧�̂̑̐�V��(�E�}�Q��)�A
�����킹�ē����闧�̂̑̐�V��(�E�}�Q��)�A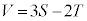 ......[��]
......[��]
(4) S�́A���ar�C����1�̉~���Ɣ��ar�̋������킹���̐ςŁA
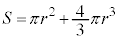 ......[��]�@����I
......[��]�@����I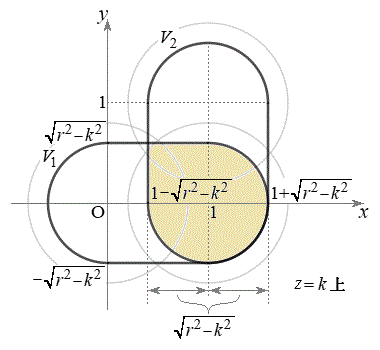 (1)�Ɠ��l�ɍl����ƁA����
(1)�Ɠ��l�ɍl����ƁA���� �C����
�C����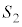 ��
��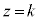 �Ő����Ƃ��̒f�ʂ̉~�̔��a��
�Ő����Ƃ��̒f�ʂ̉~�̔��a��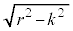 �ł��B
�ł��B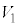 ��
��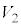 �̋��ʕ�����
�̋��ʕ�����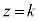 �Ő�ƒf�ʂ͉E�}�����F���F���̂悤�ɂȂ�܂��B
�Ő�ƒf�ʂ͉E�}�����F���F���̂悤�ɂȂ�܂��B
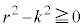 ���
���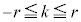 �ł����āA���̖ʐ�
�ł����āA���̖ʐ�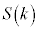 �́A1��
�́A1��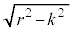 �̐����`�̖ʐςƔ��a
�̐����`�̖ʐςƔ��a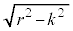 �̉~�̖ʐς�
�̉~�̖ʐς�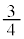 �̘a�ł����āA
�̘a�ł����āA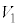 ��
��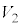 �̋��ʕ�����xy���ʂɊւ��đΏ̂�(��ϕ��Ƒ̐����Q��)�A
�̋��ʕ�����xy���ʂɊւ��đΏ̂�(��ϕ��Ƒ̐����Q��)�A����ƇI���A
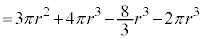
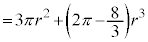 ......[��]
......[��]
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���嗝�n���wTOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2025(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B