���嗝�n���w'18�N�O��[4]
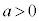 �Ƃ��A
�Ƃ��A
�Ƃ����B����2�������݂����_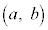 �̓�������͈͂����߁A���W���ʏ�ɐ}������B
�̓�������͈͂����߁A���W���ʏ�ɐ}������B
����1�F������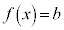 �͑��قȂ�3�����������B
�͑��قȂ�3�����������B ����2�F����ɁA������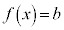 �̉���
�̉���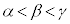 �Ƃ����
�Ƃ����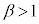 �ł���B
�ł���B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@�W���I�Ȗ��W�ɂ��ڂ��Ă���悤�Ȗ��ŁA�{��͗��Ƃ��܂���B
������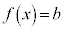 �̉��́A
�̉��́A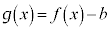 �Ƃ����āA������
�Ƃ����āA������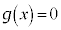 �̉��ƈ�v���܂��B
�̉��ƈ�v���܂��B
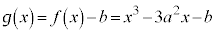 �@����@
�@����@
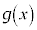 �������\�͈ȉ��̂悤�ɂȂ�܂��B
�������\�͈ȉ��̂悤�ɂȂ�܂��B
����1���A3��������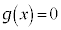 �����قȂ�3�����������̂́A�ɑ�l
�����قȂ�3�����������̂́A�ɑ�l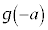 �Ƌɏ��l
�Ƌɏ��l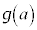 �̐ς����ɂȂ�Ƃ�(�����@�̕������ւ̉��p���Q��)�ŁA
�̐ς����ɂȂ�Ƃ�(�����@�̕������ւ̉��p���Q��)�ŁA
�܂�A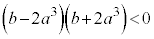 �@����A
�@����A
�̂Ƃ��ł��B
������ �̉�α�Cβ�Cγ(
�̉�α�Cβ�Cγ(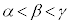 )�̂����Aβ�́A
)�̂����Aβ�́A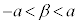 �͈̔͂ɂ���̂ŁA
�͈̔͂ɂ���̂ŁA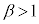 �Ƃ������Ƃ́A
�Ƃ������Ƃ́A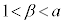 �Ƃ������Ƃł��B�܂�A����2��菭�Ȃ��Ƃ��A
�Ƃ������Ƃł��B�܂�A����2��菭�Ȃ��Ƃ��A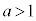 �@����B
�@����B
�܂��A�����\���A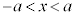 �ɂ�����
�ɂ�����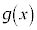 �͌����ŁA�����B�̂��ƂɁA
�͌����ŁA�����B�̂��ƂɁA �ł��邽�߂ɂ́A
�ł��邽�߂ɂ́A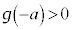 �C
�C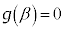 �C
�C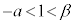 ���A
���A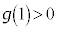 ���K�v�\���ł�(���Ԓl�̒藝���Q��)�B
���K�v�\���ł�(���Ԓl�̒藝���Q��)�B
����āA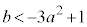 �@����C
�@����C
�B���C�̂Ƃ��A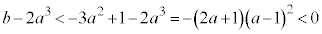 �C�A���A
�C�A���A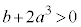
 �ȏ���A2�������݂����_
�ȏ���A2�������݂����_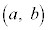 �̓�������͈͂́A�A���B���C�ŁA�C�܂��A���E���̕�����
�̓�������͈͂́A�A���B���C�ŁA�C�܂��A���E���̕�����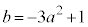 ��
��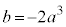 ��A������ƁA
��A������ƁA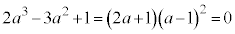 ���A���Ȑ���
���A���Ȑ��� �ɂ����Đڂ��邱�Ƃɒ��ӂ��āA
�ɂ����Đڂ��邱�Ƃɒ��ӂ��āA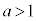 ����
����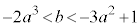 ......[��]
......[��]
�}������ƁA�E�}���ΐF���F��(���E������܂܂��A���}��������)(�̈����Q��)�B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���嗝�n���wTOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2025(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B