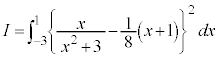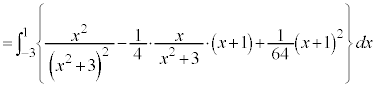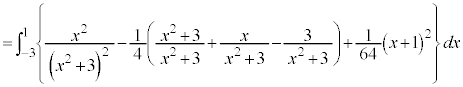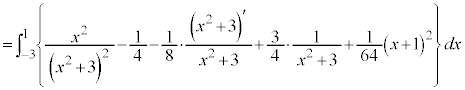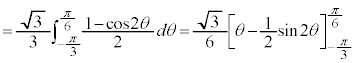東大理系数学'21年前期[3]
関数
に対して、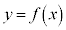 のグラフをCとする。点A
のグラフをCとする。点A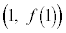 におけるCの接線を
におけるCの接線を
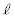 :
: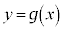
(1) Cと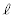 の共有点でAと異なるものがただ1つ存在することを示し、その点のx座標を求めよ。
の共有点でAと異なるものがただ1つ存在することを示し、その点のx座標を求めよ。 (2) (1)で求めた共有点のx座標をαとする。定積分
を計算せよ。
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
解答 微積分の計算問題です。(2)はあらゆるタイプの積分が登場します。難しくはないですが面倒です。慎重に計算しましょう。
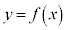 と
と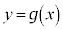 を連立して、
を連立して、分母を払って整理すると、
よって、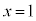 以外の解は
以外の解は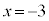 のみで、Cと
のみで、Cと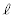 の共有点でAと異なるものがただ1つ存在し、その点のx座標は、
の共有点でAと異なるものがただ1つ存在し、その点のx座標は、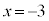 ......[答]
......[答] (2) 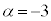 です。
です。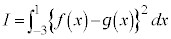 とおくと、
とおくと、 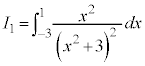 ,
,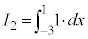 ,
,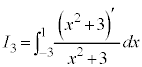 ,
,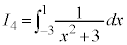 ,
,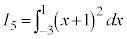 とおくと、
とおくと、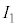 と
と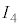 は、
は、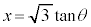 (置換積分を参照)とおいて、
(置換積分を参照)とおいて、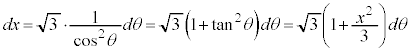 より、
より、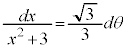 ,x:
,x: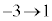 のときθ:
のときθ: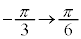 (
(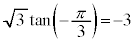 ,
,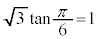 ),よって、
),よって、以上より、
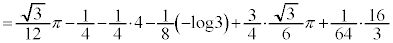
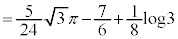 ......[答]
......[答]
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
東大理系数学TOP 数学TOP TOPページに戻る
【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。©2005-2024(有)りるらる 苦学楽学塾 随時入会受付中!理系大学受験ネット塾苦学楽学塾(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。