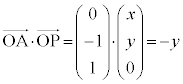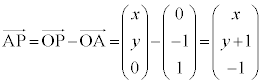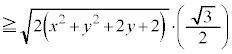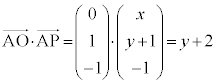���嗝�n���w'24�N�O��[1]
���W��ԓ��̓_A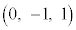 ���Ƃ�Bxy���ʏ�̓_P�����̏���(i)�C(ii)�C(iii)�����ׂĖ������Ƃ���B
���Ƃ�Bxy���ʏ�̓_P�����̏���(i)�C(ii)�C(iii)�����ׂĖ������Ƃ���B
(i) P�͌��_O�ƈقȂ�B(ii) 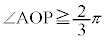
(iii) 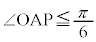
P���Ƃ肤��͈͂�xy���ʏ�ɐ}������B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@����(ii)�����_�́AO�_�Ƃ����ɐ����ɐ����f�ʂ̒��a�̗��[�ƒ��_O�ō��p��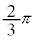 �ł���~����
�ł���~����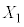 �̓����̓_�ł��B����(iii)�����_�́AA�_�Ƃ����ɐ����ɐ����f�ʂ̒��a�̗��[�ƒ��_A�ō��p��
�̓����̓_�ł��B����(iii)�����_�́AA�_�Ƃ����ɐ����ɐ����f�ʂ̒��a�̗��[�ƒ��_A�ō��p��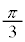 �ł���~����
�ł���~����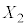 �̓����̓_�ł��B
�̓����̓_�ł��B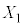 ��xy����(���_��ʂ�)�Ő�ƁA����͒����ŋ��܂ꂽ�}�`�ł��B
��xy����(���_��ʂ�)�Ő�ƁA����͒����ŋ��܂ꂽ�}�`�ł��B ��xy����(���_��ʂ�Ȃ�)�Ő�ƁA����͑ȉ~�ł�(2���Ȑ��̕������Q��)�B
��xy����(���_��ʂ�Ȃ�)�Ő�ƁA����͑ȉ~�ł�(2���Ȑ��̕������Q��)�B
xy���ʏ�̓_P�̍��W��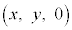 �Ƃ��܂��B
�Ƃ��܂��B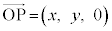 �ł��B����(i)���
�ł��B����(i)���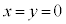 �Ƃ������Ƃ͂���܂���B
�Ƃ������Ƃ͂���܂���B
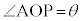 �Ƃ��āA
�Ƃ��āA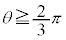 �C
�C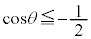 �ł��B
�ł��B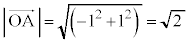 �C����(ii)���A
�C����(ii)���A
����A
����āA
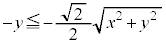 �@����@
�@����@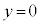 �̂Ƃ��A
�̂Ƃ��A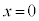 �łȂ���A�@�͐������܂���B�ł����A����(i)�����Ȃ��Ȃ�܂��B�܂��A
�łȂ���A�@�͐������܂���B�ł����A����(i)�����Ȃ��Ȃ�܂��B�܂��A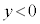 �̏ꍇ�͇@�͐������܂���B�����
�̏ꍇ�͇@�͐������܂���B�����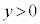 �ŁA�@�́A
�ŁA�@�́A
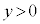 �Ƃ���2�悷��ƁA
�Ƃ���2�悷��ƁA
����āA"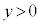 ����
����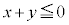 ����
����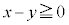 " �܂��� "
" �܂��� "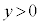 ����
����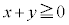 ����
����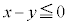 "�@����A
"�@����A
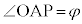 �Ƃ��āA
�Ƃ��āA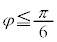 �C
�C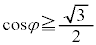 �ł��B
�ł��B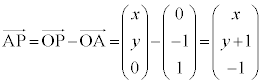
����(iii)���A
����A
����āA
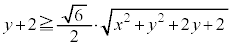 �@����B
�@����B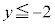 �̂Ƃ��B�͐������܂���B
�̂Ƃ��B�͐������܂���B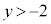 �̂Ƃ��A���ӂ�2�悵�āA
�̂Ƃ��A���ӂ�2�悵�āA
�C���ȉ~�̓�����\���܂��B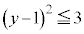 ���A�ȉ~��
���A�ȉ~��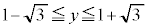 �͈̔͂ɑ��݂��܂��B
�͈̔͂ɑ��݂��܂��B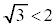 ���
���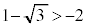 �ɒ��ӂ��܂��B�܂��ȉ~�̓����Ɍ��_���܂݂܂��B
�ɒ��ӂ��܂��B�܂��ȉ~�̓����Ɍ��_���܂݂܂��B
�C�̋��E��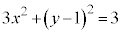 ��
��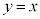 �C
�C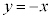 ��A������ƁA
��A������ƁA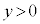 �͈̔͂ł́A
�͈̔͂ł́A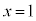 �C
�C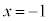
�ȉ~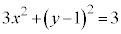 �ƒ���
�ƒ���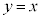 �C����
�C����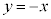 �Ƃ́A�_
�Ƃ́A�_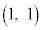 �C�_
�C�_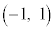 �Ō����܂��B
�Ō����܂��B
 �A�C�C���AP�̂Ƃ肤��͈͂́A"�u
�A�C�C���AP�̂Ƃ肤��͈͂́A"�u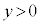 ������
������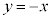 ���牺���ł����Ă�����
���牺���ł����Ă�����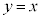 ���牺���v�܂��́u
���牺���v�܂��́u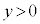 ������
������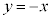 ����㑤�ł����Ă�����
����㑤�ł����Ă�����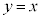 ����㑤"�ł����Ă��A"�ȉ~
����㑤"�ł����Ă��A"�ȉ~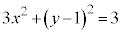 �������"�ł��B�����A�ȉ~
�������"�ł��B�����A�ȉ~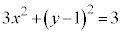 ��������ł����Ă�����
��������ł����Ă�����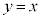 ����㑤�ł����Ă�����
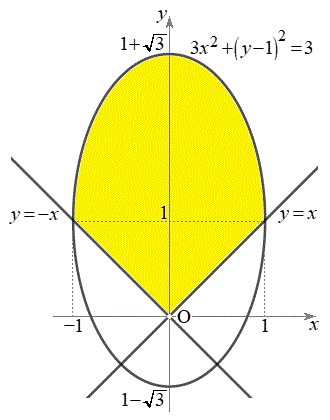
����㑤�ł����Ă�����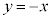 ����㑤�ɂȂ�܂�(�s�����̕\���̈����Q��)�B�}������ƁA�E�}���F���F��(���E�����܂݁A���}��������)�B
����㑤�ɂȂ�܂�(�s�����̕\���̈����Q��)�B�}������ƁA�E�}���F���F��(���E�����܂݁A���}��������)�B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���嗝�n���wTOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B