東京大学理系2024年前期数学入試問題


【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
 【広告】広告はここまでです。
[1]　座標空間内の点Aをとる。xy平面上の点Pが次の条件(i)，(ii)，(iii)をすべて満たすとする。
(i) Pは原点Oと異なる。
(ii)
(iii)
Pがとりうる範囲をxy平面上に図示せよ。
[解答へ]

[2]　次の関数を考える。
　()
(1) を満たす実数αで、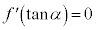となるものを求めよ。
(2) (1)で求めたαに対し、の値を求めよ。
(3) 関数の区間における最大値と最小値を求めよ。必要ならば、であることを用いてよい。
[解答へ]

[3]　座標平面上を次の規則(i)，(ii)に従って1秒ごとに動く点Pを考える。
(i) 最初に、Pは点にいる。
(ii) ある時刻でPが点にいるとき、その1秒後にはPは
・確率でx軸に関してと対称な点
・確率でy軸に関してと対称な点
・確率で直線に関してと対称な点
・確率で直線に関してと対称な点
にいる。
以下の問いに答えよ。ただし、(1)については、結論のみを書けばよい。
(1) Pがとりうる点の座標をすべて求めよ。
(2) nを正の整数とする。最初からn秒後にPが点にいる確率と、最初からn秒後にPがにいる確率は等しいことを示せ。
(3) nを正の整数とする。最初からn秒後にPが点にいる確率を求めよ。
[解答へ]

[4]　とおく。を満たす実数t に対し、座標平面上の点を通り、この点において放物線と共通の接線を持ち、x軸上に中心を持つ円をとする。
(1) 円の中心の座標を，半径をとおく。とをt の整式で表せ。
(2) 実数aはを満たすとする。円が点を通るような実数t はの範囲にいくつあるか。
[解答へ]

[5]　座標空間内に3点A，B，Cをとり、Dを線分ACの中点とする。三角形ABDの周および内部をx軸のまわりに1回転させて得られる立体の体積を求めよ。
[解答へ]

[6]　2以上の整数で、1とそれ自身以外に正の約数を持たない数を素数という。以下の問いに答えよ。
(1) とする。が素数となるような整数nをすべて求めよ。
(2) a，bを整数の定数とし、とする。が素数となるような整数nの個数は3個以下であることを示せ。
[解答へ]



【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。
 【広告】広告はここまでです。
　　東大理系数学TOP　　数学TOP　　TOPページに戻る

【広告】ここから広告です。ご覧の皆さまのご支援ご理解を賜りたく、よろしくお願いいたします。

【広告】広告はここまでです。
各問題の著作権は
出題大学に属します。
©2005-2023
(有)りるらる
苦学楽学塾 随時入会受付中！
理系大学受験ネット塾苦学楽学塾
(ご案内はこちら)ご入会は、
まず、こちらまでメールを
お送りください。