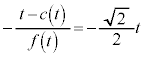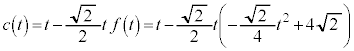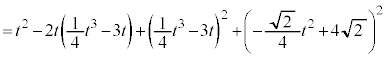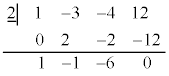���嗝�n���w'24�N�O��[4]
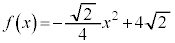 �Ƃ����B
�Ƃ����B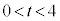 ��������t �ɑ��A���W���ʏ�̓_
��������t �ɑ��A���W���ʏ�̓_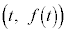 ��ʂ�A���̓_�ɂ����ĕ�����
��ʂ�A���̓_�ɂ����ĕ�����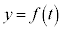 �Ƌ��ʂ̐ڐ��������Ax����ɒ��S�����~��
�Ƌ��ʂ̐ڐ��������Ax����ɒ��S�����~��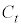 �Ƃ���B
�Ƃ���B
(1) �~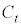 �̒��S�̍��W��
�̒��S�̍��W��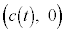 �C���a��
�C���a��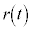 �Ƃ����B
�Ƃ����B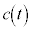 ��
��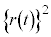 ��t �̐����ŕ\���B
��t �̐����ŕ\���B (2) ����a��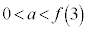 �����Ƃ���B�~
�����Ƃ���B�~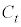 ���_
���_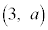 ��ʂ�悤�Ȏ���t ��
��ʂ�悤�Ȏ���t ��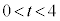 �͈̔͂ɂ������邩�B
�͈̔͂ɂ������邩�B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@�ʓ|�Ȍv�Z���ł��B
(1) �~ 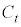 �F
�F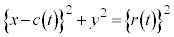 �@����@
�@����@ �~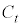 ��̓_
��̓_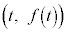 �ɂ������ڐ��́A
�ɂ������ڐ��́A 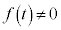 �̂Ƃ��A�ڐ��̌X���́A
�̂Ƃ��A�ڐ��̌X���́A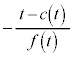 �@����A
�@����A��������̓_��y���W��0�܂�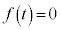 �̂Ƃ��A
�̂Ƃ��A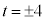
���̂Ƃ��A�~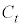 �̒��S��x����ɂ���̂ŁA�ړ_��x����ɂ���ꍇ�A�ڐ���x���ɐ����ɂȂ�܂����A
�̒��S��x����ɂ���̂ŁA�ړ_��x����ɂ���ꍇ�A�ڐ���x���ɐ����ɂȂ�܂����A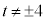 �Ȃ̂ŁA�������̐ڐ���x���ɐ����ɂȂ邱�Ƃ͂���܂���B
�Ȃ̂ŁA�������̐ڐ���x���ɐ����ɂȂ邱�Ƃ͂���܂���B
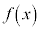 �����������ƁA
�����������ƁA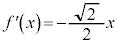
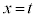 �ɂ�����������̐ڐ��̌X���́A
�ɂ�����������̐ڐ��̌X���́A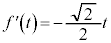 �@����B
�@����B
�~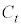 �ƕ�����
�ƕ�����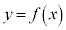 ��
��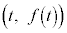 �Ƌ��ʂ̐ڐ������̂ŁA�A�ƇB����v���܂��B
�Ƌ��ʂ̐ڐ������̂ŁA�A�ƇB����v���܂��B �� 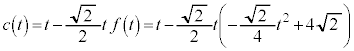
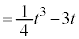 ......[��]�@����C
......[��]�@����C�܂��A�ړ_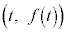 �͉~
�͉~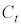 ��̓_�ł�����̂ŁA�@�����܂��B
��̓_�ł�����̂ŁA�@�����܂��B �� 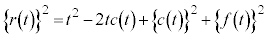
(2) �~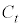 ��
��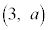 ��ʂ�̂ŁA�@��
��ʂ�̂ŁA�@��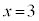 �C
�C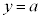 �Ƃ��āA
�Ƃ��āA �C�C�D��p���āA
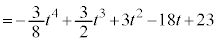 �@����E
�@����E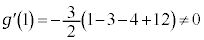 �C
�C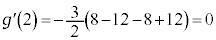
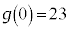 �C
�C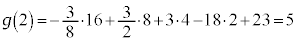 �C
�C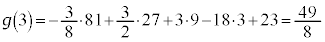 �C
�C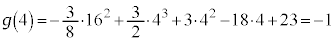 �����\�͈ȉ�
�����\�͈ȉ�| t | 0 | �@ | 2 | �@ | 3 | �@ | 4 |
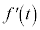 | �@ | �| | 0 | �{ | 0 | �| | �@ |
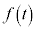 | 23 |  | 5 |  | 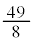 |  | 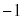 |
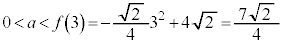 ���
���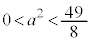
�~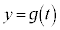 ���_
���_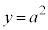 ��ʂ�Ƃ��E�F
��ʂ�Ƃ��E�F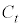 �ƂȂ�̂ŁA
�ƂȂ�̂ŁA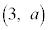 �̃O���t��
�̃O���t��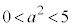 �̌�_���l����(�����@�̕������ւ̉��p���Q��)���Ƃɂ��A�~
�̌�_���l����(�����@�̕������ւ̉��p���Q��)���Ƃɂ��A�~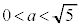 ���_
���_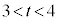 ��ʂ�悤�Ȏ���t �̌��́A
��ʂ�悤�Ȏ���t �̌��́A
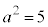 �C�����A
�C�����A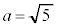 �̂Ƃ��A
�̂Ƃ��A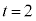 �͈̔͂�1�A
�͈̔͂�1�A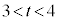 �C�����A
�C�����A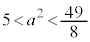 �̂Ƃ�
�̂Ƃ�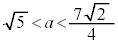 ��
��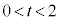 �͈̔͂�1�ō��킹��2�A
�͈̔͂�1�ō��킹��2�A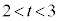 �C�����A
�C�����A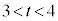 �̂Ƃ�
�̂Ƃ�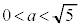 �C
�C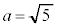 �C
�C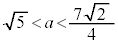 �͈̔͂ɂ��ꂼ��1�ō��킹��3�A����āA
�͈̔͂ɂ��ꂼ��1�ō��킹��3�A����āA
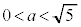 �̂Ƃ�1�A
�̂Ƃ�1�A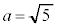 �̂Ƃ�2�A
�̂Ƃ�2�A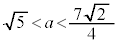 �̂Ƃ�3�� ......[��]
�̂Ƃ�3�� ......[��]
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���嗝�n���wTOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B 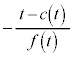 �@����A
�@����A