���嗝�n���w'24�N�O��[3]
���W���ʏ�����̋K��(i)�C(ii)�ɏ]����1�b���Ƃɓ����_P���l����B
(i) �ŏ��ɁAP�͓_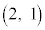 �ɂ���B
�ɂ���B (ii) ���鎞����P���_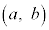 �ɂ���Ƃ��A����1�b��ɂ�P��
�ɂ���Ƃ��A����1�b��ɂ�P�� �E�m��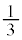 ��x���Ɋւ���
��x���Ɋւ���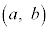 �ƑΏ̂ȓ_
�ƑΏ̂ȓ_ �E�m��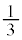 ��y���Ɋւ���
��y���Ɋւ���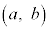 �ƑΏ̂ȓ_
�ƑΏ̂ȓ_ �ɂ���B
�ȉ��̖₢�ɓ�����B�������A(1)�ɂ��ẮA���_�݂̂������悢�B
(1) P���Ƃ肤��_�̍��W�����ׂċ��߂�B
(2) n�𐳂̐����Ƃ���B�ŏ�����n�b���P���_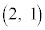 �ɂ���m���ƁA�ŏ�����n�b���P��
�ɂ���m���ƁA�ŏ�����n�b���P��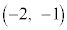 �ɂ���m���͓��������Ƃ������B
�ɂ���m���͓��������Ƃ������B (3) n�𐳂̐����Ƃ���B�ŏ�����n�b���P���_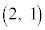 �ɂ���m�������߂�B
�ɂ���m�������߂�B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@�q���g������̂ŁA���Ƃ��Ȃ�܂��B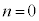 �������ӂ��K�v�ł��B
�������ӂ��K�v�ł��B
(1) A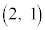 �CB
�CB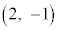 �CC
�CC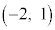 �CD
�CD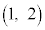 �CE
�CE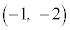 �CF
�CF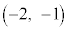 �CG
�CG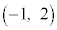 �CH
�CH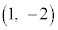 �Ƃ���ƁAA��B��x���Ɋւ��đΏ́AA��C��y���Ɋւ��đΏ́AA��D��
�Ƃ���ƁAA��B��x���Ɋւ��đΏ́AA��C��y���Ɋւ��đΏ́AA��D��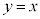 �Ɋւ��đΏ́AA��E��
�Ɋւ��đΏ́AA��E��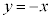 �Ɋւ��đΏ́AB��F��y���Ɋւ��đΏ́AB��G��
�Ɋւ��đΏ́AB��F��y���Ɋւ��đΏ́AB��G��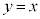 �Ɋւ��đΏ́AB��H��
�Ɋւ��đΏ́AB��H��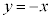 �Ɋւ��đΏ̂ł�(���W���ʂɂ�����Ώ����Q��)�B���̓_�ɑ��āA�e�Ώ̈ړ��ōs��̓_��\�ɂ܂Ƃ߂�ƁA
�Ɋւ��đΏ̂ł�(���W���ʂɂ�����Ώ����Q��)�B���̓_�ɑ��āA�e�Ώ̈ړ��ōs��̓_��\�ɂ܂Ƃ߂�ƁA | �ړ��_�_ | A | B | C | D | E | F | G | H |
| x���Ɋւ���Ώ̈ړ� | B | A | F | H | G | C | E | D |
| y���Ɋւ���Ώ̈ړ� | C | F | A | G | H | B | D | E |
����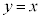 �Ɋւ���Ώ̈ړ� �Ɋւ���Ώ̈ړ� | D | G | H | A | F | E | B | C |
����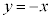 �Ɋւ���Ώ̈ړ� �Ɋւ���Ώ̈ړ� | E | H | G | F | A | D | C | B |
�]���āA�\���A��蕶�̑Ώ̈ړ��ɂ���āAA�CB�CC�CD�CE�CF�CG�CH�ȊO�̓_�ɍs�����Ƃ͂���܂���B
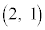 �C
�C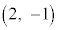 �C
�C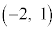 �C
�C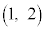 �C
�C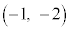 �C
�C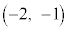 �C
�C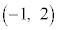 �C
�C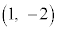 ......[��]
......[��]
(2) n�b���A�CB�CC�CD�CE�CF�CG�CH�ɂ����m����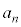 �C
�C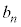 �C
�C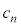 �C
�C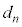 �C
�C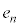 �C
�C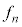 �C
�C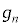 �C
�C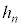 �Ƃ��܂��B
�Ƃ��܂��B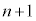 �b���A�ɗ���̂́An�b��(
�b���A�ɗ���̂́An�b��(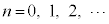 )�ɁA
)�ɁA B�ɂ���(�m��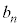 )�Ax���Ɋւ���Ώ̈ړ�(�m��
)�Ax���Ɋւ���Ώ̈ړ�(�m��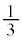 )�ŁAC�ɂ���(�m��
)�ŁAC�ɂ���(�m��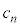 )�Ay���Ɋւ���Ώ̈ړ�(�m��
)�Ay���Ɋւ���Ώ̈ړ�(�m��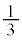 )�ŁAD�ɂ���(�m��
)�ŁAD�ɂ���(�m��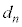 )�A����
)�A����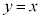 �Ɋւ���Ώ̈ړ�(�m��
�Ɋւ���Ώ̈ړ�(�m��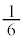 )�ŁAE�ɂ���(�m��
)�ŁAE�ɂ���(�m��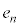 )�A����
)�A����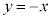 �Ɋւ���Ώ̈ړ�(�m��
�Ɋւ���Ώ̈ړ�(�m��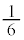 )�ŁAA�ɂ���ꍇ�ł��B�����m��
)�ŁAA�ɂ���ꍇ�ł��B�����m��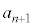 �́A
�́A 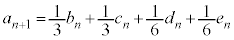 �@����@
�@����@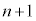 �b���F�ɗ���̂́AC��F(�m��
�b���F�ɗ���̂́AC��F(�m��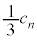 )�CB��F(�m��
)�CB��F(�m��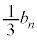 )�CE��F(�m��
)�CE��F(�m��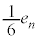 )�CD��F(�m��
)�CD��F(�m��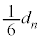 )�̏ꍇ�ŁA���̊m��
)�̏ꍇ�ŁA���̊m��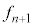 �́A
�́A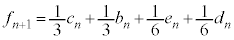 �@����A
�@����A�@�C�A���A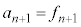 (
(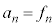 )�]���āAn�𐳐����Ƃ���
)�]���āAn�𐳐����Ƃ���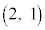 �C�����A�ŏ�����n�b���P���_
�C�����A�ŏ�����n�b���P���_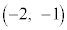 �ɂ���m���ƁA�ŏ�����n�b���P��
�ɂ���m���ƁA�ŏ�����n�b���P��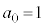 �ɂ���m���͓������Ȃ�܂��B
�ɂ���m���͓������Ȃ�܂��B ���D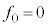 �C
�C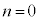 �Ȃ̂ŁA
�Ȃ̂ŁA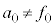 �̏ꍇ�́A
�̏ꍇ�́A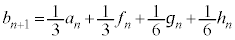 �ł��B�܂��A
�ł��B�܂��A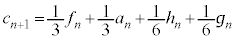 �Ȃ̂ŁA
�Ȃ̂ŁA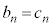 �ł��B
�ł��B
(3) �@�C�A�Ɠ��l�ɂ��āA(1)�̕\���A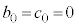 �Ƃ��āA
�Ƃ��āA ����āAn�𐳐����Ƃ���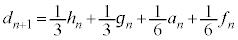 �CB��C�ɂ��ẮA
�CB��C�ɂ��ẮA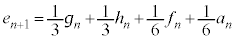 �Ȃ̂ŁA
�Ȃ̂ŁA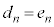 �ɂ���
�ɂ���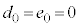 �ł��B
�ł��B ����āAn�𐳐����Ƃ���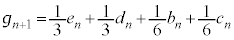 �CD��E�ɂ��ẮA
�CD��E�ɂ��ẮA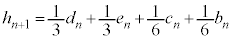 �Ȃ̂ŁA
�Ȃ̂ŁA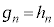 �ɂ���
�ɂ���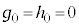 �ł��B
�ł��B ����āAn�𐳐����Ƃ���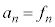 �CG��H�ɂ��ẮA
�CG��H�ɂ��ẮA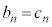 �Ȃ̂ŁA
�Ȃ̂ŁA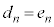 �ɂ���
�ɂ���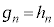 �ł��Bn�𐳂̐����Ƃ��āA
�ł��Bn�𐳂̐����Ƃ��āA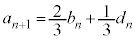 �C
�C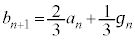 �C
�C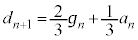 �C
�C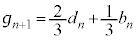
�����p���āA��L�Q����������������ƁAn�𐳂̐����Ƃ��āA 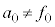 �@����B
�@����B
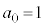 �@����C
�@����C
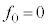 �@����D
�@����D
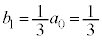 �@����E
�@����E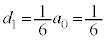 (
(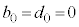 �C
�C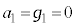 )�Ȃ̂ŁA�K��(ii)���A
)�Ȃ̂ŁA�K��(ii)���A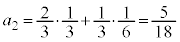 �C
�C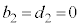 �ł��B�܂��A
�ł��B�܂��A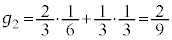 �Ȃ̂ŁA
�Ȃ̂ŁA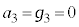 �ł��B
�ł��B
�����ŁA��̕��ׂĂ����ƁA�ƂȂ��Ă��āA�K����������̂��킩��܂��B���������ƁA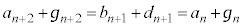 ��
��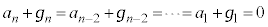 ��g�ݍ��킹��Ƃ悳�����ł��B
��g�ݍ��킹��Ƃ悳�����ł��B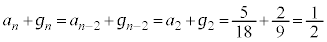 �̌W���A
�̌W���A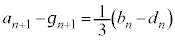 �̌W�����B�ƇE�œ���ւ���Ă���̂ŁA�A���Q�����̒�ɏ]���āA�B�{�E�ƇB�|�E���l���܂��B
�̌W�����B�ƇE�œ���ւ���Ă���̂ŁA�A���Q�����̒�ɏ]���āA�B�{�E�ƇB�|�E���l���܂��B
�B�{�E���A 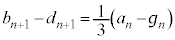 �@����F
�@����F�C�{�D���A
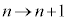 �@����G
�@����G�F��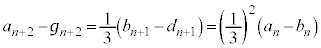 �Ƃ���ƁA�G���A
�Ƃ���ƁA�G���A n�𐳂̊�Ƃ��āA
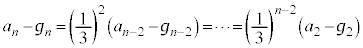 �@����H
�@����Hn�𐳂̋����Ƃ��āA
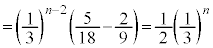 �@����I
�@����I�B�|�E���A
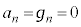 �@����J
�@����J�C�|�D���A
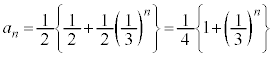 �@����K
�@����K�J��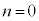 �Ƃ���ƁA�K���A
�Ƃ���ƁA�K���A n�𐳂̊�Ƃ��āA
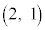 �@����L
�@����Ln�𐳂̋����Ƃ��āA
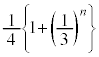 �@����M
�@����Mn�����̊�̂Ƃ��A�H�C�L���A
n�����̋����̂Ƃ��A�I�{�M���A
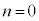 �̂Ƃ�
�̂Ƃ�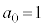 �ł��B
�ł��B
�ȏ���A�ŏ�����n�b���P���_A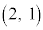 �ɂ���m���́An�����̊�̂Ƃ�0�Cn�����̋����̂Ƃ�
�ɂ���m���́An�����̊�̂Ƃ�0�Cn�����̋����̂Ƃ�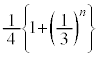 ......[��]
......[��]
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���嗝�n���wTOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B 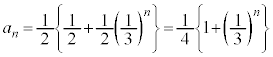
 ......[��]
......[��]