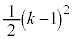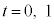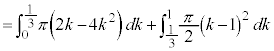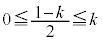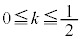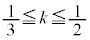���嗝�n���w'24�N�O��[5]
���W��ԓ���3�_A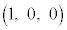 �CB
�CB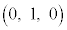 �CC
�CC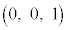 ���Ƃ�AD�����AC�̒��_�Ƃ���B�O�p�`ABD�̎�����ѓ�����x���̂܂���1��]�����ē����闧�̂̑̐ς����߂�B
���Ƃ�AD�����AC�̒��_�Ƃ���B�O�p�`ABD�̎�����ѓ�����x���̂܂���1��]�����ē����闧�̂̑̐ς����߂�B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
���@����ɂ��Ă͊ȒP�Ȗ�肾�Ȃ��A�Ǝv���Ă���Ǝv��ʊ��v���҂��Ă��܂��B
AB�̒��_D�́A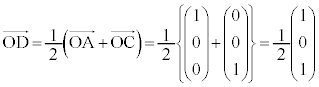 �@(�x�N�g���̓����E�O�����Q��)
�@(�x�N�g���̓����E�O�����Q��)
�O�p�`ABD�̕ӂƂȂ�x�N�g�������߂�ƁA
�O�p�`ABD�̕ӏ�̓_�̈ʒu�x�N�g�������߂܂��B
�_P������DB��ɂ���Ƃ��A����DB��̓_P�̈ʒu�x�N�g��(�����̃x�N�g�����������Q��)�́A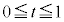 �Ƃ��āA
�Ƃ��āA
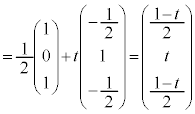 �@����@
�@����@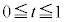 �Ƃ��āA
�Ƃ��āA
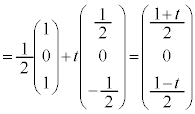 �@����A
�@����A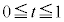 �Ƃ��āA
�Ƃ��āA
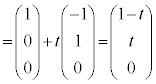 �@����B
�@����B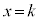 �Ő�Ƃ��ɁA�O�p�`DAB�̊e�ӂƂ̌�_�����߂܂��B
�Ő�Ƃ��ɁA�O�p�`DAB�̊e�ӂƂ̌�_�����߂܂��B
�@�ɂ����āA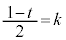 �Ƃ���ƁA
�Ƃ���ƁA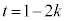 �C������@�ɑ�����āA��DB�ƕ���
�C������@�ɑ�����āA��DB�ƕ���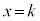 �̌�_��H
�̌�_��H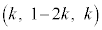 �ł��B�����ŁA
�ł��B�����ŁA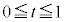 ���
���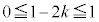 �C����
�C����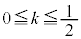 �ł��B
�ł��B
�A�ɂ����āA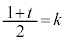 �Ƃ���ƁA
�Ƃ���ƁA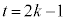 �C������@�ɑ�����āA��DA�ƕ���
�C������@�ɑ�����āA��DA�ƕ���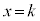 �̌�_��I
�̌�_��I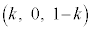 �ł��B�����ŁA
�ł��B�����ŁA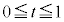 ���
���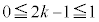 �C����
�C����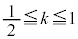 �ł��B
�ł��B
�B�ɂ����āA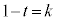 �Ƃ���ƁA
�Ƃ���ƁA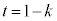 �C������@�ɑ�����āA��DA�ƕ���
�C������@�ɑ�����āA��DA�ƕ���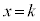 �̌�_��J
�̌�_��J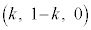 �ł��B�����ŁA
�ł��B�����ŁA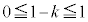 �C����
�C����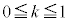 �ł��B
�ł��B
����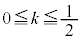 �́A
�́A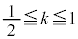 �̂Ƃ���DB��H�Ō����A
�̂Ƃ���DB��H�Ō����A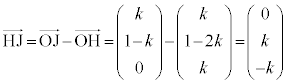 �̂Ƃ���DA��I�Ō����A
�̂Ƃ���DA��I�Ō����A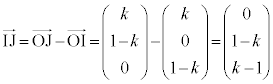 �̂Ƃ���AB��J�Ō����܂����A����ŁAH��J�C���邢��I��J�̂����A��]�����牓�����̓_����]�������~�̖ʐς���߂����̓_����]�������~�̖ʐς�������k�Őϕ��A�Ƃ���Ă��܂��̂�����ł��B
�̂Ƃ���AB��J�Ō����܂����A����ŁAH��J�C���邢��I��J�̂����A��]�����牓�����̓_����]�������~�̖ʐς���߂����̓_����]�������~�̖ʐς�������k�Őϕ��A�Ƃ���Ă��܂��̂�����ł��B
����HJ�C����IJ��̓_�ŁA��]������ł��߂��_���A�����̒[�_�ɂȂ�Ƃ͌���Ȃ�����ł�(��]�̂̑̐����Q��)�B
�����ŁA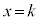 �̂Ƃ��A
�̂Ƃ��A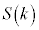 �̂Ƃ��A�ɕ����āA����HJ��̓_�A����IJ��̓_�ŁA��]������ł��߂��_�A�ł������_���l���邱�ƂɂȂ�܂��B
�̂Ƃ��A�ɕ����āA����HJ��̓_�A����IJ��̓_�ŁA��]������ł��߂��_�A�ł������_���l���邱�ƂɂȂ�܂��B
��L���AH�CI�CJ�̍��W�́AH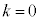 �CI
�CI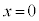 �CJ
�CJ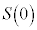 �Ȃ̂ŁA
�Ȃ̂ŁA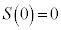 �̂Ƃ��A
�̂Ƃ��A
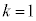 �@����C
�@����C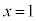 �̂Ƃ��A
�̂Ƃ��A
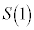 �@����D
�@����D
�O�p�`ABD����]�����Ăł��闧�̂�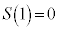 �Ő����Ƃ��̒f�ʐς�
�Ő����Ƃ��̒f�ʐς�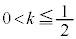 �Ƃ��܂��B
�Ƃ��܂��B
�E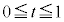 �̂Ƃ��A����
�̂Ƃ��A����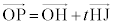 �ƎO�p�`ABD�Ƃ̋��L�_�͓_B�����ł��B�_B����]�������Ƃ��̒f�ʐ�
�ƎO�p�`ABD�Ƃ̋��L�_�͓_B�����ł��B�_B����]�������Ƃ��̒f�ʐ�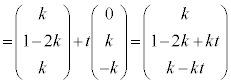 ��
��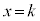 �ƍl���܂��B
�ƍl���܂��B �E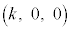 �̂Ƃ��A����
�̂Ƃ��A����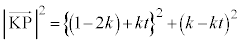 �ƎO�p�`ABD�Ƃ̋��L�_�͓_A�����ł��B�_A����]�������Ƃ��̒f�ʐ�
�ƎO�p�`ABD�Ƃ̋��L�_�͓_A�����ł��B�_A����]�������Ƃ��̒f�ʐ�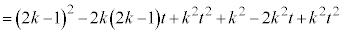 ��
��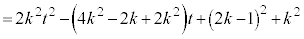 �ƍl���܂��B
�ƍl���܂��B �E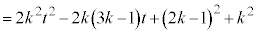 �̂Ƃ��A����HJ��̓_P�̈ʒu�x�N�g���́A
�̂Ƃ��A����HJ��̓_P�̈ʒu�x�N�g���́A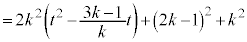 �Ƃ��āA�C���A
�Ƃ��āA�C���A ����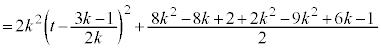 �̉�]����̓_K
�̉�]����̓_K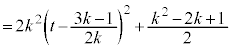 ��P�Ƃ̋�����2���(�������Q��)�A
��P�Ƃ̋�����2���(�������Q��)�A 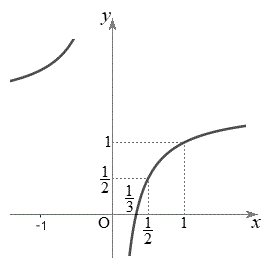 �E�}���A
�E�}���A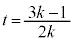 �̃O���t��`���Ă݂�ƁA
�̃O���t��`���Ă݂�ƁA(a) 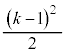 �̂Ƃ��At ��2����
�̂Ƃ��At ��2����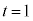 �̎��̈ʒu��
�̎��̈ʒu��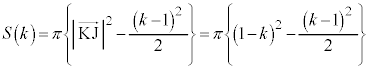 �ƂȂ�A2����
�ƂȂ�A2����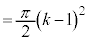 �́A
�́A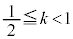 (P��H�ɗ���)�̂Ƃ��ŏ���
(P��H�ɗ���)�̂Ƃ��ŏ���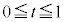 (P��J�ɗ���)�̂Ƃ��ő�ɂȂ�܂�(2�����̍ő�ŏ����Q��)�B
(P��J�ɗ���)�̂Ƃ��ő�ɂȂ�܂�(2�����̍ő�ŏ����Q��)�B (b) 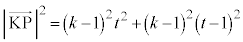 �̂Ƃ��A2����
�̂Ƃ��A2����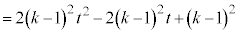 �̎��̈ʒu�́A
�̎��̈ʒu�́A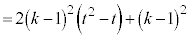 �ƂȂ�A2����
�ƂȂ�A2����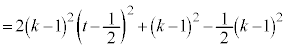 �́A
�́A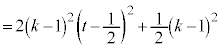 �̂Ƃ��ɍŏ��l
�̂Ƃ��ɍŏ��l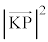 ���Ƃ�A
���Ƃ�A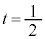 (P��J�ɗ���)�̂Ƃ��ő�ɂȂ�܂��B
(P��J�ɗ���)�̂Ƃ��ő�ɂȂ�܂��B 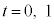
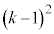 �@����F
�@����F�E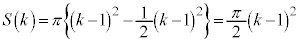 �̂Ƃ��A����IJ��̓_P�̈ʒu�x�N�g���́A
�̂Ƃ��A����IJ��̓_P�̈ʒu�x�N�g���́A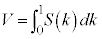 �Ƃ��āA�D���A
�Ƃ��āA�D���A ����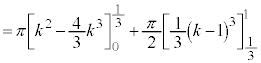 �̉�]����̓_K
�̉�]����̓_K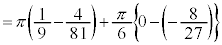 ��P�Ƃ̋�����2��́A
��P�Ƃ̋�����2��́A 2����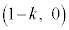 �́A
�́A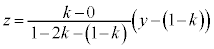 �̂Ƃ��ŏ��l
�̂Ƃ��ŏ��l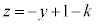 ���Ƃ�A
���Ƃ�A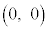 �̂Ƃ�(P���[�_I�CJ�ɗ���)�ő�l
�̂Ƃ�(P���[�_I�CJ�ɗ���)�ő�l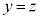 ���Ƃ�܂��B
���Ƃ�܂��B 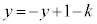 �@����G
�@����G
�E�C�F�C�G�C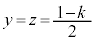 ���A���߂��̐�V�́A
���A���߂��̐�V�́A
�ʉ��D��L�ł́A�����ɉ�]������A����HJ��̓_�Ƃ̋����̍ő�ŏ��A����IJ��̓_�Ƃ̋����̍ő�ŏ����l���܂������A����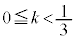 ��ōl���邱�Ƃ��ł��܂��B��L���A
��ōl���邱�Ƃ��ł��܂��B��L���A 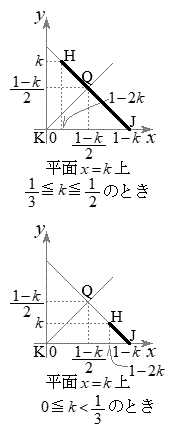 �E
�E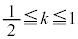 �̂Ƃ��A����
�̂Ƃ��A����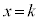 ��ŁAH
��ŁAH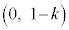 �CJ
�CJ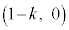 �ł�(�E�}�Q��)�B����HJ��(�����̕��������Q��)�A
�ł�(�E�}�Q��)�B����HJ��(�����̕��������Q��)�A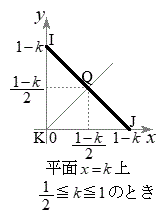 �E
�E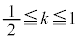 �̂Ƃ��A����
�̂Ƃ��A����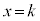 ��ŁAI
��ŁAI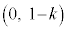 �CJ
�CJ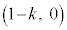 �ł��B(�E�}�Q��)���̂Ƃ��́AK
�ł��B(�E�}�Q��)���̂Ƃ��́AK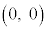 �������IJ�ɐ���KQ��K���������Ƃ��ł��āAK����̋����̍ŏ��l��
�������IJ�ɐ���KQ��K���������Ƃ��ł��āAK����̋����̍ŏ��l��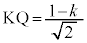 �C�ő�lKJ�ł��B
�C�ő�lKJ�ł��B
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�@�@���嗝�n���wTOP�@�@���wTOP�@�@TOP�y�[�W�ɖ߂�
�y�L���z��������L���ł��B�����̊F���܂̂��x�������������肽���A��낵�����肢�������܂��B
�y�L���z�L���͂����܂łł��B
�e���̒��쌠��
�o���w�ɑ����܂��B©2005-2024(�L)����� ��w�y�w�m ���������t���I���n��w�l�b�g�m��w�y�w�m(���ē���������)������́A
�܂��A������܂Ń��[����
�����肭�������B 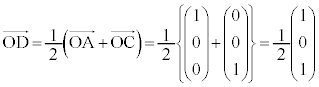 �@
�@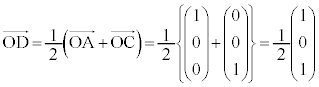 �@(�x�N�g���̓����E�O�����Q��)
�@(�x�N�g���̓����E�O�����Q��)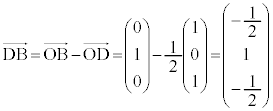
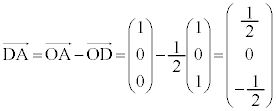
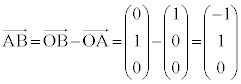
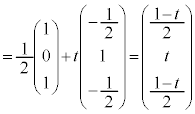 �@����@
�@����@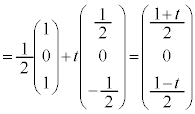 �@����A
�@����A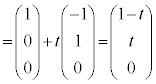 �@����B
�@����B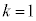 �@����C
�@����C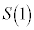 �@����D
�@����D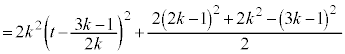
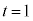
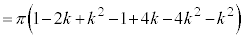
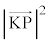
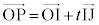
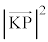 ���Ƃ�A
���Ƃ�A